St. Petersburg, Russian Federation
St. Petersburg, Russian Federation
student
St. Petersburg, Russian Federation
UDC 69.059.22
CSCSTI 67.01
Russian Library and Bibliographic Classification 308
The objective of this article is to develop the theoretical foundations for assessing the load-bearing capacity of structures using the vibration method, to establish the exact value of the position of the neutral line during the operation of reinforced concrete structures. The following methods were used in the study: mathematical modeling based on known theoretical expressions and comparison of the obtained results with experimental data. The paper considered structures with different levels of load-bearing capacity, namely a beam without defects, a beam with small cracks, and a beam with a main crack. The obtained experimental values of the residual height of the concrete cross-section and the height of the compressed zone quite accurately coincide with the data of mathematical modeling for these characteristics. The results obtained will allow us to approach the solution of the problem of theoretical justification of the vibration method of inspection of reinforced concrete structures, improve the methods of its implementation and improve the accuracy of the results obtained.
load-bearing capacity, vibration method, reinforced concrete structures, defects
Широкое применение железобетонных конструкций (ЖБК) в качестве несущего остова зданий началось примерно с 60-х годов прошлого века и насчитывает более 70 лет. За столь длительный период эксплуатации в конструкциях появились дефекты различного типа. В настоящее время, одним из актуальных вопросов является вопрос оценки их технического состояния в соответствии с ГОСТ 31937-2024. Использование современных приборов неразрушающих методов контроля позволяет определять лишь физико-механические характеристики ЖБК, и потом с помощью расчётных формул оценивать их несущую способность. Одним из способов оценивания несущей способности конструкций, без применения расчётных методов, является вибрационный метод [1–3].
Для теоретического обоснования вибрационного метода неразрушающего контроля железобетонных конструкций [1, 4], путем измерения частот колебаний и геометрических параметров конструкции необходимо точно понимать в какой степени в работе данной ЖБК задействованы ее элементы. Какая доля нагрузки приходится на бетон, а какая на арматуру?
Ключевым параметром для определения этих соотношений является положение нейтральной линии сечения, или высота сжатой зоны бетона x [3,5]. Расчеты этого параметра, согласно нормативной документации, позволяют рассчитать значение нейтральной линии для состояния близкого к разрушению конструкции, что не приемлемо для целей диагностики.
Согласно СП 63.13330.2018 пространственная жесткость железобетонной балки определяется по формуле:
|
|
(1) |
где
| $$ k_b=\frac{0,15}{\phi_I\cdot(0,3+\delta_e)} $$ |
где ϕl — коэффициент, учитывающий влияние длительности действия нагрузки;
Запишем уравнение жесткости сечения железобетонной балки относительно уровня нейтрального слоя, так как поворот сечения осуществляется именно относительно этой линии.
| $$I(x)=\frac{b}{3}\cdot x^3+[(h_0-\delta)-x]^3,$$ |
(2) |
| $$ I_s(x)=I_{sc}+I_s+A'_{sx}-a'2+A_sh_0-x^2, $$ |
(3) |
где x — высота сжатой зоны;
δ — глубина трещины;
Значения
Подставив выражения (2), (3) в исходное выражение (1) получаем формулу для оценки жесткости железобетонной балки в зависимости от положения нейтрального слоя или высоты сжатой зоны бетона:
|
$$D=k_bE_b\frac{b}{3} \cdot (x^3+[(h_0-\delta)-x]^3+k_sE_s(A'_s(x-a')^2+A_s(h_0-x)^2),$$ |
(4) |
Для удобства записи введем коэффициенты
|
|
(5) |
|
|
(6) |
|
$$a_3=\frac{k_bE_bb(h_0-\delta)^3}{3}+k_sE_s(A'_sa'^2+A_sh^2_0).$$ |
(7) |
Конечное уравнение запишем в виде:
|
|
(8) |
Для примера возьмём железобетонную балку 1ПБ-10-1П, характеристики которой представлены в Таблице 1. Схема загружения и сечение балки представлено на Рис. 1 и 2 соответственно.
Таблица 1
Оценка эффективности компонентов добавки
|
Марка |
Размеры, мм |
Масса, кг |
Es, МПа |
Eb, МПа |
|||||||||
|
L |
L0 |
b |
b' |
h |
h0 |
a |
a' |
d |
δ |
||||
|
1ПБ-10-1П |
1030 |
930 |
120 |
80 |
65 |
53 |
12 |
18 |
4 |
Var(0…h0) |
20 |
3х |
2х |
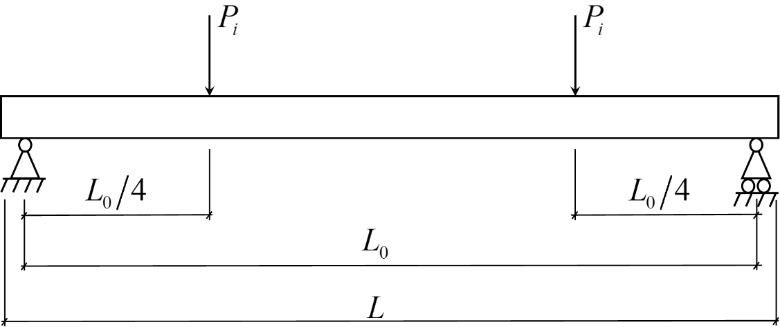
Рис. 1. Расчетная схема балки 1 ПБ-10-1П
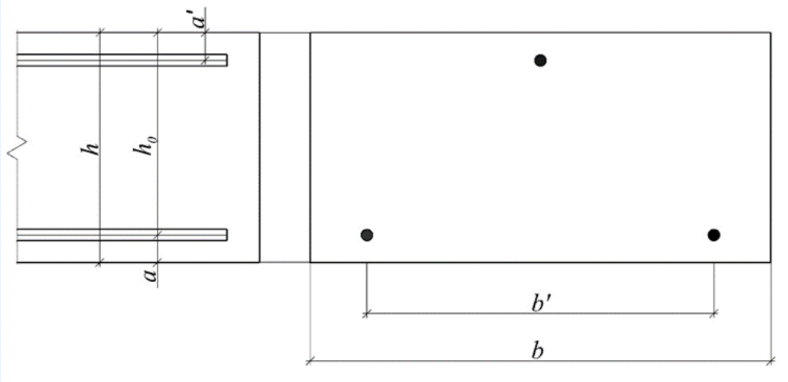
Рис. 2. Сечение балки 1 ПБ-10-1П
Применим уравнение (8) к исходной балке и определим те состояния, в которых жесткость достигает своих минимальных/максимальных значений и не может выходить за отведенные границы.
Уравнение (8) является квадратным, график которого представляет собой параболу, ветви которой направлены вверх, а вершина имеет координаты (m, n), где
| $$m=-\frac{-a_2}{2 \cdot a_1},$$ |
(9) |
|
$$n=-\frac{a_2^2-4 \cdot a_1 \cdot a_3}{4 \cdot a_1},$$ |
(10) |
Необходимо найти экстремумы функции D(x,

Рис 3. Область допустимых значений высоты сжатой зоны бетона
Назовем трещины, глубина которых попадает в 1 и 2 области трещинами первого и второго типа соответственно, и исследуем распределение напряжений в сечении и высоту сжатой зоны бетона. Для этого смоделируем в программном комплексе «ELCUT» данные случаи (Рис. 4–6), рассматривая железобетонную балку как упруго-деформируемую систему.
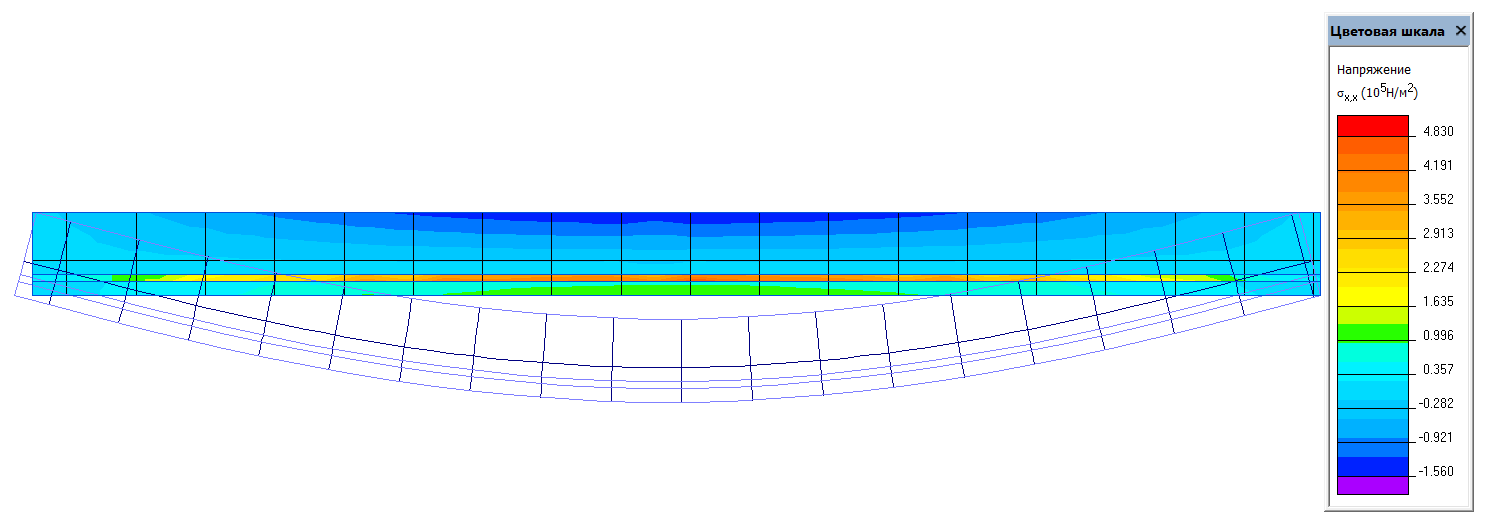
Рис. 4. Модель балки без трещин
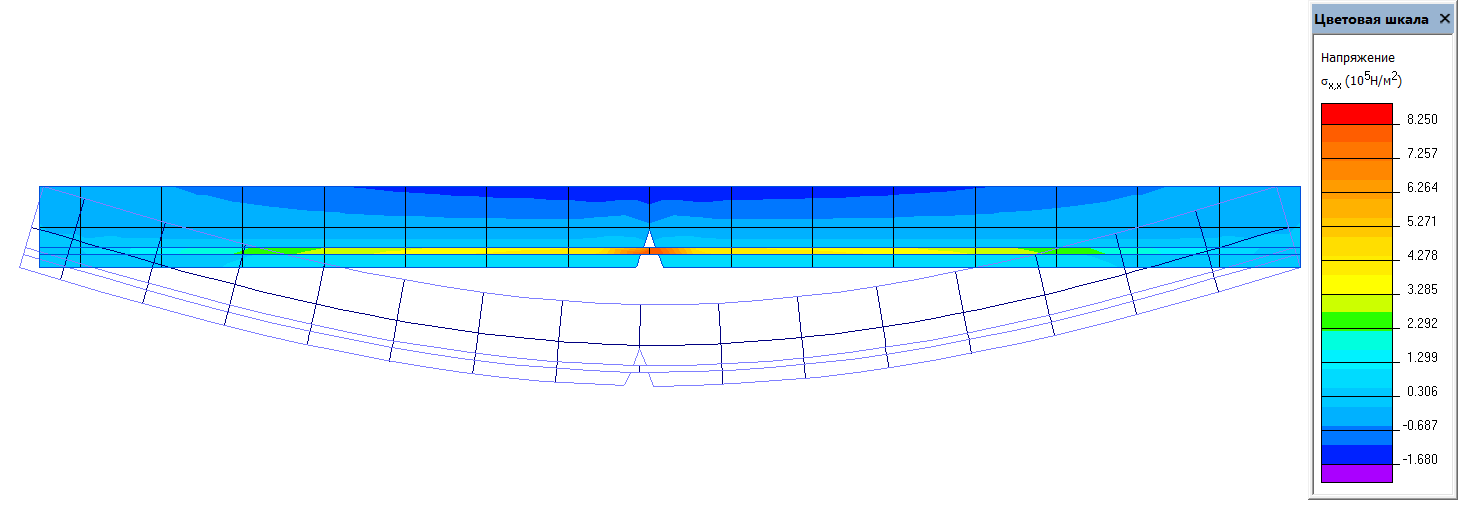
Рис. 5. Модель балки с трещиной первого типа
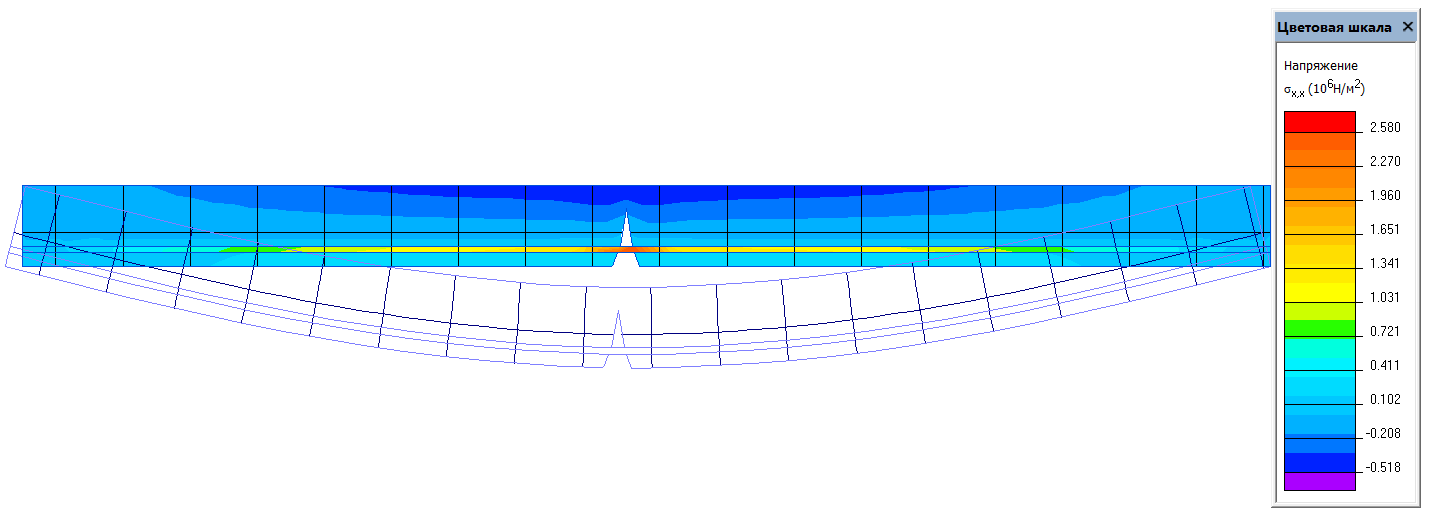
Рис. 6. Модель балки с трещиной второго типа
Полученные результаты представлены в Табл. 2.
Таблица 2
Результаты исследования
|
Тип трещины |
Результаты моделирования |
Результаты теоретического расчета |
|||
|
Глубина |
Остаточная высота |
Высота сжатой |
Максимальное значени |
Минимальное значение |
|
|
Без трещины |
- |
60,00 |
29,65 |
53,00 |
30,00 |
|
Первый тип |
23,00 |
37,00 |
27,33 |
35,00 |
27,00 |
|
Второй тип |
43,00 |
17,00 |
15,31 |
17,00 |
0,00 |
Вывод: таким образом, с использованием математических зависимостей, были определены границы нахождения фактического значения высоты сжатой зоны бетона x, которые подтверждаются моделированием с использованием метода конечных элементов.
Полученные результаты позволят приблизиться к решению задачи теоретического обоснования вибрационного метода обследования железобетонной конструкции, усовершенствования методов его проведения и повышения точности получаемых результатов.
1. Iskhakov Sh.Sh., Kovalev F.E., Mokhnatkin A.P., Starchukov D.S. Formation and development of vibration monitoring systems for the technical condition of load–bearing elements of launch facilities. 2015. 110 p.
2. Iskhakov Sh. Sh., Kovalev F. E., Sarin S. V. On the effectiveness of the method of vibration diagnostics of elements of the construction part of launch facilities // Proceedings of Tula State University. Technical sciences. 2018. I. 10. Pp. 431-441. EDN: https://elibrary.ru/YRBIPR
3. Iskhakov Sh. Sh., Kovalev F. E., Sarin S. V. Accounting for concrete cracking in vibration diagnostics of span reinforced concrete structures // Proceedings of the Military Space Academy named after A. F. Mozhaisky. 2018. I. 663. Pp. 99-104.
4. Iskhakov Sh. Sh., Kovalev F.E., Kosenkov R.E., Mokhnatkin A.P. Problems of assessing the reliability and safety of operated structures of ground-based space infrastructure and identification of their technical conditions // Izvestiya PGUPS. 2016. Vol. 13, I. 4(49). Pp. 592-599. EDN: https://elibrary.ru/YFUDFR
5. Kovalev F.E., Mokhnatkin A.P. Methodology for estimating the pre-limit and limit states of span reinforced concrete structures of launch facilities according to the height parameter of the compressed concrete zone. // Proceedings of the Military Space Academy named after A.F.Mozhaisky. 2022. No. 681. Pp. 170-175. EDN: https://elibrary.ru/BXPNZC



















