graduate student from 01.09.2015 until now
Volgograd, Volgograd, Russian Federation
employee
Volgograd, Volgograd, Russian Federation
employee
Volgograd, Volgograd, Russian Federation
GRNTI 67.01 Общие вопросы строительства
BBK 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
The results of the study of the influence of the rigidity of the soil base on the dynamic characteristics of structures, namely the frequency, modal mass, oscillation forms are given. Two types of structural solutions of structures are considered: symmetrical in plan with respect to one axis of the building and symmetric in plan with respect to two axes of the building. The parameters for modeling the stiffness dynamic characteristics of different types of soil bases are determined.
soil bases stiffness, deformation modulus of the soil bases stiffness, dynamic characteristics, frequencies, mode shapes, modal masses, symmetry, optimal stiffness of the structure.
В процессе проектирования зданий и сооружений, возводимых в сейсмоопасных районах, постоянно возникает задача о нахождении оптимальной жёсткости сооружения. Известна связь жёсткости самих конструкций и их узлов с динамическими характеристиками сооружения [7], а также влияние жёсткости (податливости) основания на частоты и формы колебаний[9, 13]. Разработаны методики по компоновке в плане сейсмоустойчивых зданий и сооружений [6]. Но возникает вопрос: есть ли такое отношение жёсткости сооружения к жёсткости основания, при котором динамические характеристики здания были бы не в ущерб его надёжности? Начать решать данный вопрос можно с обратной стороны, предварительно проанализировав динамические характеристики зданий с постоянной жёсткостью при изменении податливости основания.
В программном комплексе ЛИРА 10.6 был произведён расчёт двух вариантов условных 5-этажных зданий.
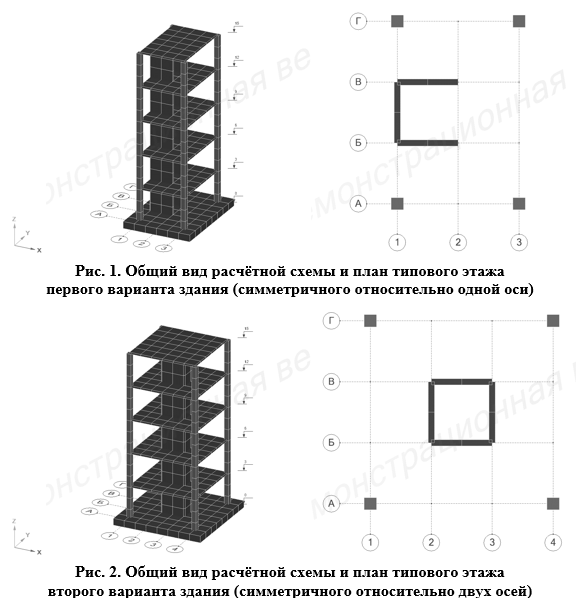
Первый вариант (рис. 1) — здание симметричное в плане относительно оси, параллельной глобальной оси X. Размер здания в плане — 4×6 м при шаге осей 2 м; высота этажа — 3 м. Фундамент условного сооружения представляет собой плиту толщиной 60 см; вертикальные конструкции представлены квадратными в сечении колоннами размером 40×40 см и стенами толщиной 20 см; горизонтальные конструкции представляют собой плиты перекрытий толщиной 16 см. Материал всех конструкций — бетон класса B30[4].
Второй вариант (рис. 2) — здание симметричное в плане относительно двух глобальных осейX и Y. Размер здания в плане — 6×6 м при шаге осей 2 м. Высота этажа, сечения фундамента, колонн, стен, плит перекрытий и материал конструкций — такие же, как и в первом варианте.
В расчётной схеме были использованы конечные элементы КЭ 44 и КЭ 10.
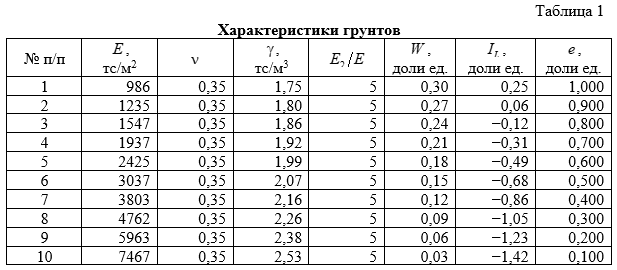
Расчёт производился на пять загружений [2]: собственный вес, постоянное загружение, полезное загружение, сейсмическое воздействие вдоль осейX и Y. Было выполнено по десять вариантов расчёта каждого здания с различными параметрами жёсткости основания [12].Принята модель Пастернака с двумя коэффициентами постели, вычисляемые по следующим динамическим характеристикам грунта: модуль деформации E, тс/м2, коэффициент поперечной деформации (Пуассона) 
, удельный вес 
, тс/м3, коэффициент перехода ко второму модулю деформации, природная влажность W, показатель текучести 
, коэффициент пористости
.
Были использованы коэффициенты пористостии модули деформации 
аллювиальных полутвёрдых суглинков (
) при степени водонасыщения 
, приведённых в таблице А.3 приложения А СП 22.13330.2016 «Основания зданий и сооружений»[3]. Для вычисления значений коэффициентов пористости и модулей деформации, отличных от табличных, предварительно аппроксимировали их функцией вида 
. Выполнив аппроксимацию и вычислив коэффициенты a и b, вывели функцию зависимости модуля деформации грунта E, тс/м2 от коэффициента пористости 
. Коэффициент корреляции такой функции равен −0,9996.
Остальные требуемые характеристики были вычислены по общеизвестным из механики грунтов формулам [5, 11], задавшись степенью влажности 
, влажностью на границе раскатывания 
, числом пластичности
и плотностью частиц грунта 
(из опыта проектирования). Полученные характеристики «виртуального» грунта представлены в таблице 1.
По результатам расчётов получены значения частот и модальных масс 15 форм колебаний для первого варианта здания (рис. 3) и 20 форм колебаний для второго (рис. 6), то есть такое количество форм, чтобы их сумма модальных масс составляла более 90 %. Для анализа рассматриваются только наиболее значимые формы, модальная масса которых более 5 %. Частоты и модальные массы таких форм для первого варианта приведены соответственно в таблицах 2 и 3, а для второго варианта — в таблицах 4 и 5.
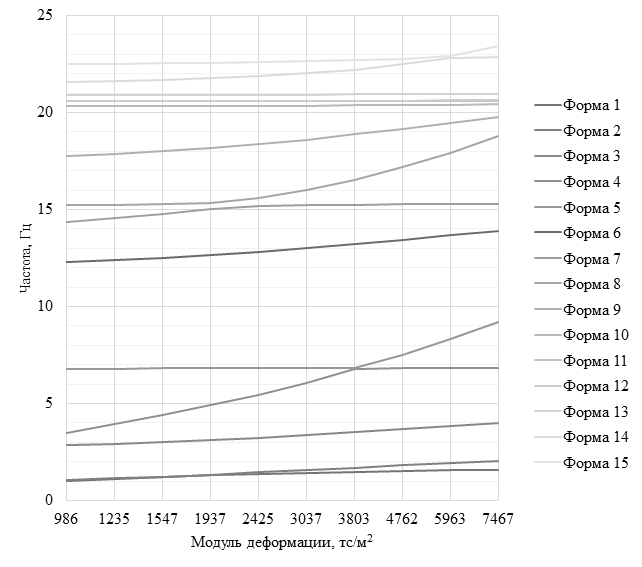
Рис. 3. Зависимость частоты колебаний от модуля деформации
первого варианта здания (симметричного относительно одной оси)
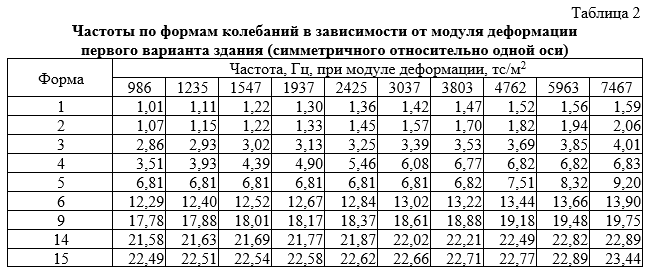
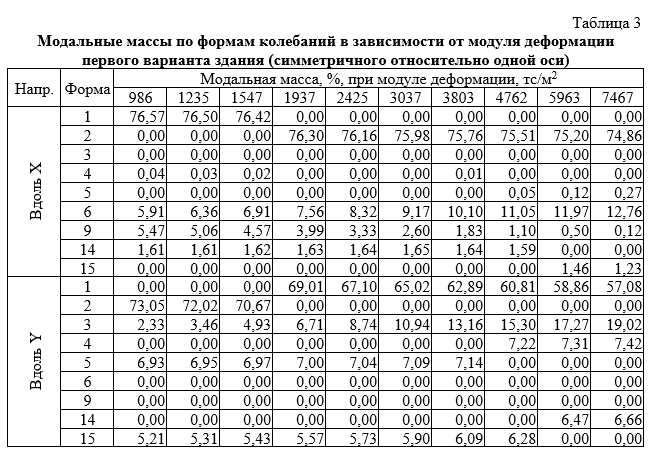
Для симметричного относительно одной оси здания во всех случаях при данной жёсткости основания частоты и формы колебаний одинаковы независимо он направления сейсмического воздействия. Различаются только модальные массы. При увеличении жесткости основания (при динамическом модуле деформации грунта 7467 тс/м2) происходит изменение соотношений между формами колебаний. Так 1-я изгибная вдоль оси X форма стала 2‑ой (рис. 5, б), а изгибная вдоль оси Y 2‑ая форма (рис. 4, б) стала 1‑ой, приобретя ещё и кручение (рис. 5, а). Эта новая 1‑ая форма имеет большой вклад при направлении сейсмического воздействия вдоль Y(модальная масса 57,08 %), что свидетельствует о нерациональной компоновке (асимметрии) и о недостаточной жёсткости сооружения по отношению к жёсткости основания. Анализируя графики частот и данные об их вкладах в общую картину колебаний здания, можно сделать вывод, что обмен позициями форм произошёл при жёсткостях основания между 1547 и 1937 тс/м2. Аналогичный взаимообмен позициями происходит соответственно между формами 4 и 5 (рис. 4, г и д, рис. 5, г и д), 14 и 15 (рис. 4, з и и, рис. 5, з и и). Форма 6 не только сохранила свою позицию (рис. 4, е, рис. 5, е), но и увеличила свой вклад с 5,91 до 12,76 % при направлении сейсмического воздействия вдоль X. Однако у 6‑ой формы сменился порядковый номер формы-партнёра, которая заменяла бы её при воздействии вдоль Y: форма 5 стала формой 4 (как было указано выше). Новая вклинившаяся между ними форма 5 (по виду ранее форма 4) имеет модальную массу, близкую к нулю.
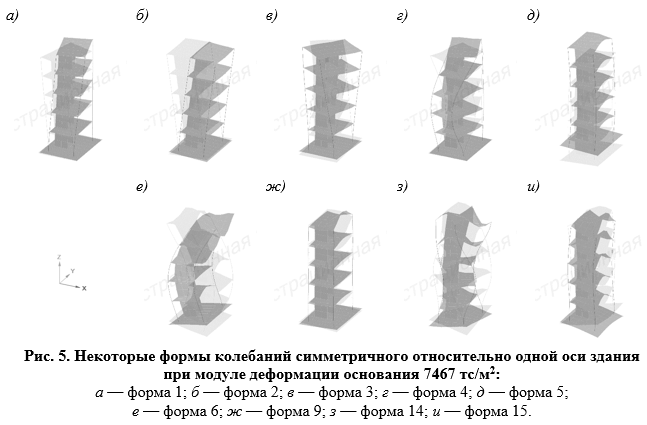
Из всего ряда выделяются только формы 3 и 9. Это формы-одиночки, так как они не имеют каких-либо форм-соседей, заменявших бы их по вкладу при другом (перпендикулярном) направлении сейсмического воздействия. Форма 3 (рис. 4, в, рис. 5, в) является чисто крутильной относительно оси Z и значима лишь при направлении сейсмического воздействия вдоль оси Y, то есть в направлении асимметрии сооружения. С увеличением жёсткости основания влияние данной формы только возрастает: модальная масса изменяется от 2,33 % при модуле деформации грунта 986 тс/м2 до 19,02 % при 7467 тс/м2. Форма 9 (рис. 4, ж, рис. 5, ж) представляет собой вертикальные колебания плит перекрытий. Данная форма значима при направлении сейсмического воздействия вдоль оси X, но с увеличением жёсткости основания её вклад падает с 5,47 % до 0,12 %.
Для симметричного относительно двух осей здания имеют место быть те же явления, что и для симметричного относительно одной оси. Также во всех случаях при данной жёсткости основания частоты и формы колебаний одинаковы независимо он направления сейсмического воздействия. Но в силу симметрии имеется одна особенность: формы-партнёры (то есть те формы, которые дополняли бы друг друга по вкладу при взаимно перпендикулярных направлениях сейсмического воздействия) имеют одинаковые частоты. По сути, это одночастотные формы. Форма 1 (рис. 7, а, рис. 8, а) является изгибной вдоль оси Y, а форма 2 — изгибной вдоль оси X (рис. 7, б, рис. 8, б). Обе формы имеют одинаковые частоты: от 1,16 Гц при жёсткости основания 986 тс/м2 до 2,29 Гц при 7467 тс/м2. При направлении сейсмического воздействия вдоль X вклады данных форм по отдельности при изменении жёсткости основания непостоянны. Модальная масса формы 1 колеблется в пределах от 0,07 % до 9,30 %, формы 2 — от 65,56 % до 75,37 %. Но сумма модальных масс 1‑ой и 2‑ой форм изменяется плавно в пределах от 75,43 % до 74,86 %.
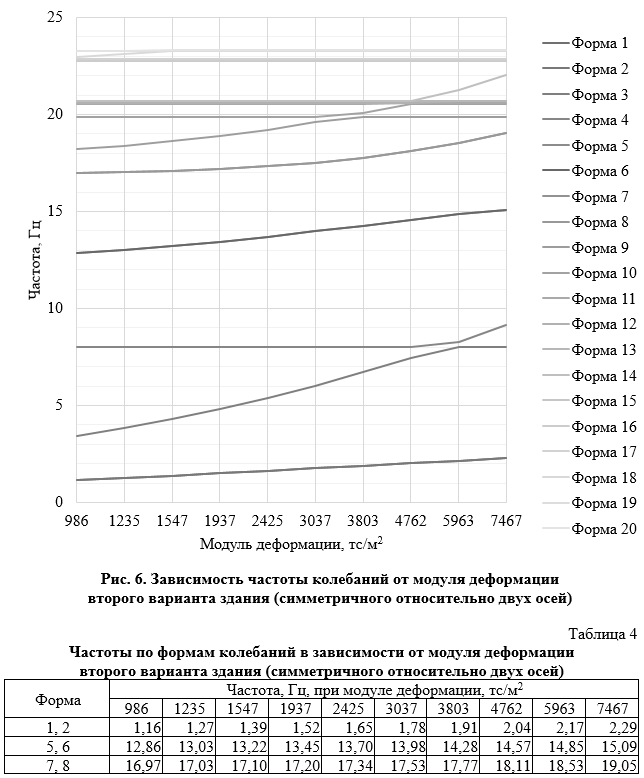
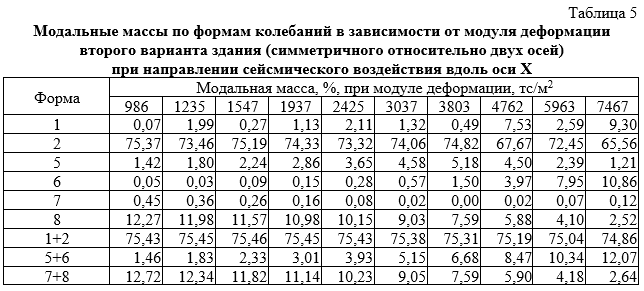
Аналогично ситуация обстоит с формами-партнёрами 5 и 6 (частоты от 12,86 до 15,09 Гц), 7 и 8 (частоты от 16,97 до 19,05 Гц). Формы 5 и 6 (рис. 7, в и г, рис. 8, в и г, изгибные в виде полной длины волны во взаимно перпендикулярных направлениях) с увеличением жёсткости основания меняются порядковыми номерами, но ввиду равности частот это роли не играет — их суммарный вклад плавно изменяется в пределах от 1,46 % до 12,07 %.Суммарный вклад форм 7 и 8 (рис. 7, д и е, рис. 8, д и е) плавно уменьшается с 12,72 % до 2,64 %.
В симметричном относительно двух осей здании крутильные формы присутствуют. Такие формы, как правило, являются формами-одиночками, так как не имеют такой же по частоте формы и формы, заменяющей её при другом направлении воздействия. Но так как данные формы никак себя не проявили (их вклад при любом направлении сейсмического воздействия близок к нулю), то в данной работе интерес не представляют.
По результатам сравнительного анализа динамических характеристик двух сооружений, а именно видов, частот и модальных масс форм колебаний, можно произвести следующую классификацию этих форм.
Формы-партнёры, как правило, имеют изгибный характер (в соответствующих нормальных друг другу направлениях) и значимы при сонаправленном внешнем воздействии. Они могут иметь как близкие частоты (например,формы 1 и 2 для симметричного относительно одной оси здания), так и далёкие (формы 5 и 6). Также между формами-партнёрами может вклиниться третья форма (форма 5 между формами 4 и 6 при более жёстком основании первого варианта сооружения) с практически нулевым вкладом. При рациональной компоновке в плане и жёсткости сооружения по отношению к жёсткости основания изгибные формы-партнёры свойственны низшим (первым) формам.
Одночастотные формы — частный случай пар форм-партнёров. Они обладают теми же свойствами в части взаимодополнения по вкладам при перпендикулярных направлениях воздействия с тем отличием, что имеют одинаковые частоты. Одночастотные пары форм свойственны зданиям, симметричным относительно двух осей, причём квадратных в плане.
Формы-одиночки — такие формы, которые не имеют какой-либо близкой по позиции и (или) частоте формы, заменяющей её при другом (перпендикулярном) направлении воздействия. Как правило, они имеют крутильный характер и проявляют себя при определённом (или близком к нему) направлении сейсмической нагрузки.
Таким образом, при проектировании сейсмостойких зданий и сооружений большое внимание следует уделять не только частотам и их вкладам, но и характерам форм колебаний. Следует добиваться таких объёмно-планировочных решений и жёсткостных характеристик здания, чтобы на низших (первых) формах наибольший вклад имели формы-партнёры изгибного характера. Очевидно, что это достигается при бо́льшем отношении жёсткости сооружения к жёсткости основания, так как при уменьшении этого отношения начинают проявлять себя крутильные формы (формы-одиночки).Другой вопрос — это численное выражение этого отношения и, следовательно, определение той грани, за которой всё большее значение имеют крутильные формы. Ответ на данный вопрос решит задачу оптимальной жёсткости сооружения и, как следствие, проблему проектирования оптимального сейсмостойкого здания и оценки надёжности таких зданий известными методами [8, 10].
1. SP 14.13330.2014. Stroitel'stvo v seysmicheskih rayonah. Aktualizirovannaya redakciya SNiP II 7 81*. Izd. oficial'noe. M.: Minstroy Rossii, 2014.
2. SP 20.13330.2016. Nagruzki i vozdeystviya. Aktualizirovannaya redakciya SNiP 2.01.07 85*. Izd. oficial'noe. M.: Minstroy Rossii, 2016.
3. SP 22.13330.2016. Osnovaniya zdaniy i sooruzheniy. Aktualizirovannaya redakciya SNiP 2.02.01 83*. Izd. oficial'noe. M.: Minstroy Rossii, 2016.
4. SP 63.13330.2012. Betonnye i zhelezobetonnye konstrukcii. Osnovnye polozheniya. Aktualizirovannaya redakciya SNiP 52 01 2003. Izd. oficial'noe. M.: Minregion Rossii, 2012.
5. GOST 25100-2011. Grunty. Klassifikaciya. Izd. oficial'noe. M.: Standartinform, 2013.
6. ISO 3010:2001. Osnovy rascheta konstrukciy. Seysmicheskie vozdeystviya na konstrukcii.
7. Volgin G.A., Rozhkov A.F., Inzhutov I.S., Goncharov Yu.M. Chislenno-eksperimental'noe issledovanie dinamicheskih parametrov krupnopanel'nogo zdaniya // Vestnik TGASU, 2016. № 3. S. 111-120.
8. Drozdov V.V., Pshenichkina V.A., Evtushenko S.I. Inzhenernaya metodika ocenki seysmicheskoy nadezhnosti zdaniy po predel'no dopustimomu risku // Vestnik VolgGASU, 2013. № 2 (27). S. 10.
9. Galiullin R.R., Izotov V.S., Nurieva D.M. Chislennye issledovaniya dinamicheskih harakteristik zdaniy s zhelezobetonnym karkasom // Izvestiya KazGASU. 2011. № 2 (16). S. 81-85.
10. Pshenichkina V.A. Nadezhnost' zdaniy kak prostranstvennyh sostavnyh sistem pri seys-micheskih vozdeystviyah : monografiya; pod. red. V.A. Pshenichkinoy. Volgograd: VolgGASU, 2010.
11. Cytovich N.A. Mehanika gruntov (kratkiy kurs) :ucheb. dlya stroit. vuzov. 4 oe izd., pere-rab. i dop. M.: Vyssh. shk., 1983.
12. Vvedenie v programmnyy kompleks LIRA 10.4 : ucheb. posobie / O.A. Koval'chuk, A.V. Kolesnikov, E.M. Rusanova [i dr.]. M.: NIU MGSU, 2015.
13. Osnovaniya, fundamenty i podzemnye sooruzheniya / M.I. Gorbunov-Posadov, V.A, Il'ichev, V.I. Krutov i dr.; pod obsch. red. E.A. Sorochana i Yu.G. Trofimenkova. M.: Stroyizdat, 1985.
