Novocherkassk, Rostov-on-Don, Russian Federation
GRNTI 27.35 Математические модели естественных наук и технических наук. Уравнения математической физики
GRNTI 67.01 Общие вопросы строительства
OKSO 01.04.03 Механика и математическое моделирование
BBK 221 Математика
BBK 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
TBK 6154 Математическое моделирование
The article proposes a mathematical modeling of the rapid flow spreading in the wide downstream of the culvert depending on the flow rate, the relative expansion of the downstream and the depth of the water at the outlet of the round pipe. An open water flow is considered in a non-pressure spreading mode. When the Froude numbers are large than four in the channel with a relative expansion of b = 3–7, pairing is established according to the type of free flow of a two-dimensional turbulent flow, the depths and flow rates at each point, the geometry of the free flow zone are determined. The flow parameters are calculated at any point of the free flow area using the Maple software package. The adequacy of the model extreme current line with the experimental one is shown.
rapid open flow, pipes of circular and rectangular cross-section, free flow.
Надежность дорожных и мелиоративных трубчатых водопропускных сооружений во многом зависит от гидравлических условий работы их нижних бьефов, где возникают сложные пространственные формы сопряжения бурного потока.
Метод расчета заключается в сведении задачи к выбору эквивалентной ширины прямоугольной трубы. Задача определения параметров потока за прямоугольной трубой решена в работах [1,2,3]. Однако в практике строительства дорожных водопропускных сооружений применяются в основном трубы круглого сечения. Это доказывает актуальность настоящей работы. Актуальность работы также подтверждается и тем, что необходимо получить аналитические, удобные для пользователей зависимости по определению параметров потока в окрестности выхода потока из трубы с адекватностью реальному процессу, превышающей адекватность по имеющимся в настоящее время методикам [4,5,6]. В работах [1,2,3] показано, что решение задачи зависит от критерия Фруда 
на выходе потока из трубы, а именно: решение при 
отличается от решения при 
Определение глубины потока на его выходе из круглой трубы и эквивалентной ширины потока за прямоугольной трубой
При заданном расходе потока 
и выбранном диаметре трубы d согласно методике в справочной литературе по гидравлике [7] определяется параметр расхода для прямоугольных труб 
. Далее из графика зависимости [7] определяется глубина потока на выходе из трубы
Параметры 
являются исходными для решения задачи определения всего комплекса параметров потока за круглой трубой.
По величинам 
и d определим площадь живого сечения потока 
по формулам в [8] (см. рис. 1 а), б)). На рисунке 1 а) показано живое сечение потока в безнапорном режиме работы трубы при 
а на рис. 1 б) живое сечение потока в полунапорном режиме при 
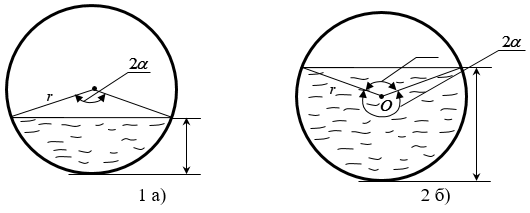
Рис. 1 Схема к определению площади живого сечения на его выходе из трубы
Для безнапорного режима течения
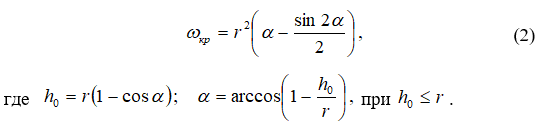
Для полунапорного режима течения
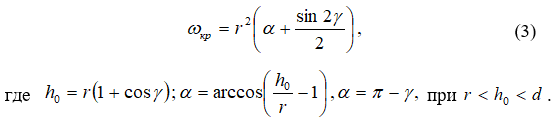
Эквивалентная ширина прямоугольной трубы определяется из условия совпадения площадей живых сечений на выходе потока из круглой и соответствующей прямоугольной труб:
Определение максимального угла растекания потока вдоль крайней верхней линии тока
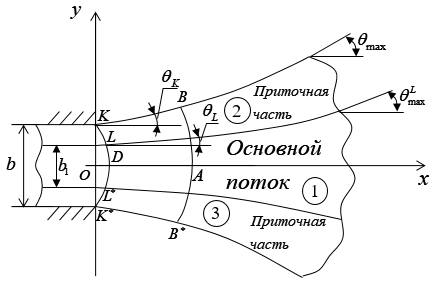
Рис. 2 План растекания потока за эквивалентной прямоугольной трубой.
эквивалентная ширина прямоугольной трубы всего потока;
ширина трубы основного потока;
Разделим, условно, живое сечение потока в круглой трубе на основное и приточное (см. рис. 2, 3)
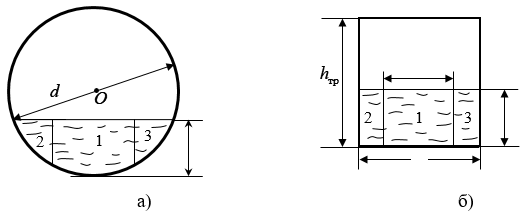
Рис. 3 Выделение в круглой трубе и соответственно в прямоугольной участков, формирующих основной поток и его приточную часть – 2, 3
Сечение 1 (рис. 3 а) формирует за круглой трубой основной поток. По форме сечение 1 мало отличается от прямоугольника. Сечения 2 и 3 формируют приточные части. Их особенность заключается в том, что они примыкают к основному сечению и возмущения, возникающие в них, распространяются в потоке независимо от основной его части. На рис. 3 б) показаны участки, соответствующие участкам на рис. 3 а).
Модуль скорости на выходе потока из трубы определим по формуле:
Тогда параметр кинетичности потока на его выходе из трубы :
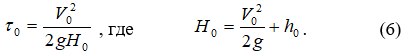
Рассматриваем случай, когда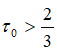 
и соответственно число Фруда 
. Максимальный угол растекания потока вдоль линии тока, ограничивающей основной поток, определим по методу, изложенному в работах [1,2,3]:
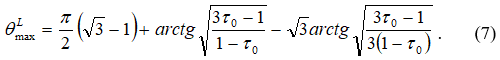
Далее определим параметры потока 
в точке 
. Согласно теории в работах [1,2,3] эти параметры определяются решением системы уравнений:
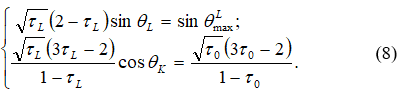
Решение системы уравнений (8) сводится к решению следующего уравнения пятой степени [9]:
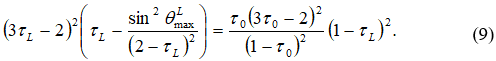
Уравнение (9) имеет единственное решение при 
. Решается это уравнение численно с использованием пакетов прикладных программ Maple или Mathcad.
Острый угол 
определяется выражением
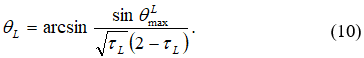
Максимальный угол растекания всего потока вдоль крайней верхней линии тока (рис. 2) определим из уравнения эпициклоиды, проходящей через точки 
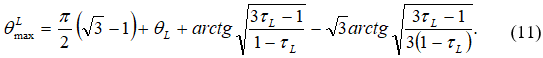
Определение параметров потока в точке 
(рис. 2)
Параметры потока в точке 
определяются решением следующей системы уравнений:
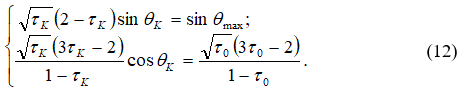
Решение системы (12) сводится к решению уравнения относительно 
аналогично уравнению (9). После нахождения корня 
угол 
определяется по формуле
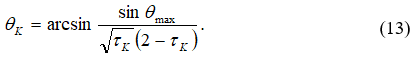
Далее при расчете параметров потока за эквивалентной прямоугольной трубой необходимо использовать результаты решения задачи, приведенные в работе [9]. В настоящей работе приведем метод определения параметров потока 
в точках крайней верхней линии тока и в точках на оси симметрии потока, а также метод определения координат этих точек (рис. 4)
Определение параметров потока 
на крайней линии тока
Параметры потока 
вдоль крайней линии тока удовлетворяют следующей системе уравнений (рис. 4):
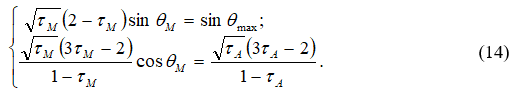
где 
значение параметра 
в точке 
, через которую проходит эквипотенциаль 
.
Значение 
задается глубиной потока в точке :
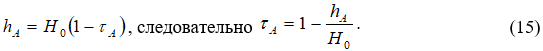
Метод решения системы (14) аналогичен методу решения системы (12).
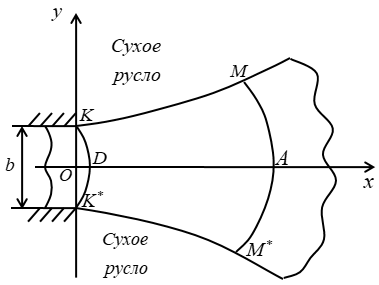
Рис. 4 План растекания потока
KM крайняя линия тока;
AM произвольная эквипотенциаль, проходящая через точки A и M
Определение координат точек A и M, в которых известны параметры 
Из содержания работы [9] известно, что справедлива следующая дифференциальная связь между дифференциалами dx,dy, дифференциалом 
и параметром 
вдоль крайней линии тока:
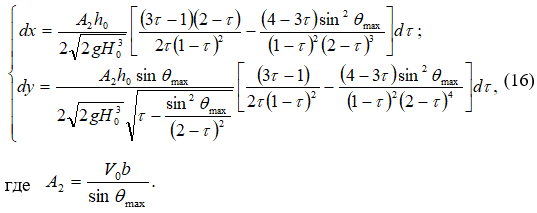
Вдоль оси симметрии потока справедлива дифференциальная связь
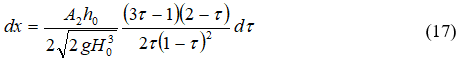
Интегрированием системы (16) найдем координаты точки M:
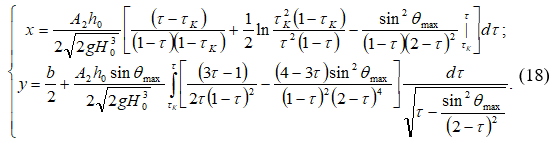
Интегрируя уравнение (17), получим абсциссу точки A на оси потока
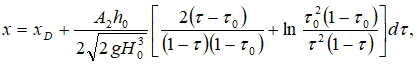
где 
определяется по формулам, приведенным в работах [1,2,3,8].
Вычисление интеграла в правой части выражения для 
в (18)
Так как вдоль крайней верхней линии тока
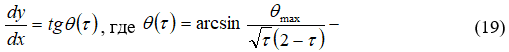
острый угол, то методы численного интегрирования для определения 
во втором уравнении из (20) даны в [10]. Пусть
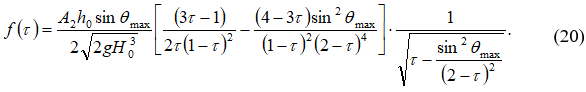
Интегрируя второе уравнение системы (16), получим
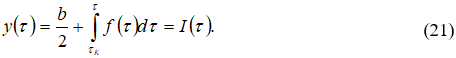
Для вычисления интеграла 
воспользуемся последовательно формулами:
правило трапеций;
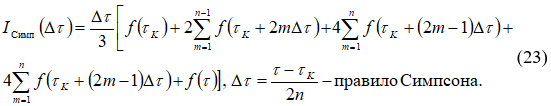
Вычисления проводились с относительной погрешностью 
В результате было установлено, что для вычисления интеграла (21) с заданной погрешностью можно пользоваться формулой Симпсона с шагом 
, или меньшим. Погрешность вычисления интеграла определялась по правилу Рунге – Ромберга [11]
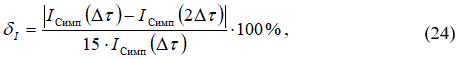
где 
- значение интеграла, вычисленное по формуле Симпсона с шагом 
;
- значение интеграла, вычисленное с двойным шагом.
Сравнение формы (геометрии) крайних линий тока:
модельных и экспериментальных
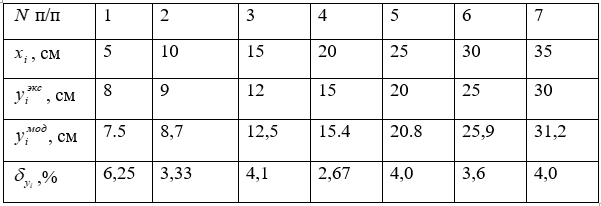
Результаты экспериментов взяты из работы [12]. Исходные данные для определения модельных и экспериментальных значений ординат 
.
1). Диаметр трубы 
2). Максимальная глубина потока на выходе из трубы 
3). Скорость потока на выходе из трубы 
.
Таблица 1
Координаты крайней линии тока свободно растекающегося потока и рассогласование с экспериментом
Выводы по работе
1. Метод аналитического определения параметров свободно растекающегося водного потока в окрестности его выхода из круглой трубы оправдан логически и подтверждается высокой степенью сходимости по параметрам потока: реального и модельного.
2. Численные методы расчета интегралов в работе с использованием правила Симпсона и оценки погрешности результатов модели и экспериментов показывают приемлемость методов.
1. Kokhanenko V.N. Modelirovanie odnomernykh i dvukhmernykh otkrytykh vodnykh potokov [Simulation of one-dimensional and two-dimensional open water flows]. Rostov-on-Don: YuFU Publ., 2007. 168 p.
2. Kokhanenko V.N. Modelirovanie burnykh dvukhmernykh v plane vodnykh potokov [Simulation of two-dimensional turbulent in terms of water flows]. Rostov-on-Don: YuFU Publ., 2013. 180 p.
3. Shiryaev V.V. Razvitie teorii dvukhmernykh otkrytykh vodnykh potokov [The development of the theory of two-dimensional open water flows]. Shakhty: YuRGUES Publ., 2007. 133 p.
4. Sherenkov I.A. O planovoy zadache rastekaniya strui burnogo potoka neszhimaemoy zhidkosti [On the planned problem of the spreading of a jet of a turbulent flow of an incompressible fluid]. Izvestiya AN SSSR. OTN [News of the USSR Academy of Sciences. REL]. 1958, I. 1, pp. 72-78.
5. Lilitskiy G.A. Issledovaniya rastekaniya burnogo potoka v nizhnem b’efe vodopropusknykh sooruzheniy [Studies of the spreading of the turbulent flow in the downstream of the culverts]. Gidravlika i gidrotekhnika [Hydraulics and hydraulic engineering]. Kiev: Tekhnika Publ., 1966, I. 2, pp. 78-84.
6. Mishchuk G.Ya. Opredelenie polya skorostey v plane rastekashchegosya burnogo potoka metodom kharakteristik [Determination of the velocity field in terms of spreading turbulent flow by the method of characteristics]. Izvestiya vuzov, «Ener-References getika» [Proceedings of universities, “Energy”]. Minsk, 1963, I. 10.
7. Spravochnik po gidravlike [Handbook of hydraulics]. Kiev: Vishcha shkola Publ., 1984. 343 p.
8. Korn G. Spravochnik po matematike dlya nauchnykh rabotnikov i inzhenerov [Handbook of mathematics for scientists and engineers]. Moscow: Nauka Publ., 1970. 720 p.
9. Mitsik M.F., Kosichenko N.V., Lemeshko M.A. Metod s ispol’zovaniem godografa skorosti primenitel’no k raschetu parametrov burnogo dvukhmernogo potoka [The method using the speed hodograph as applied to the calculation of the parameters of a rapid two-dimensional flow]. Matematicheskoe i komp’yuternoe modelirovanie estestvennonauchnykh i sotsial’nykh problem [Mathematical and computer simulation of natural science and social problems]. Penza: Privolzhskiy Dom znaniy Publ. 2010, pp. 130-141.
10. Samarskiy A.A. Chislennye metody [Numerical methods]. Moscow, Nauka Publ. 1989. 432 p.
11. Berezin I.S., Zhidkov N.P. Metody vychisleniy [Calculation methods]. Moscow, GIFML Publ., 1959, V. 1, 620 p.
12. Kol’chenko O.L. Upravlenie kinematicheskoy strukturoy dvukhmernogo burnogo potoka za trubchatymi vodosbrosnymi sooruzheniyami. Kand. Diss. [Management of the kinematic structure of a two-dimensional turbulent flow behind tubular spillway structures. Cand. Diss.]. Kiev, 1987. 20 p.
