Rostov-na-Donu, Rostov-on-Don, Russian Federation
Rostov-na-Donu, Rostov-on-Don, Russian Federation
Russian Federation
GRNTI 67.23 Архитектурно-строительное проектирование
GRNTI 67.01 Общие вопросы строительства
OKSO 270000 АРХИТЕКТУРА И СТРОИТЕЛЬСТВО
BBK 385 Строительные конструкции
BBK 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
TBK 5414 Строительные конструкции
The article deals with the modeling of wind impact on the building of complex parametric shape. Several variants of finite element models have been developed- beam and beam-free floor slabs with cantilever overhangs, bearing elements in the form of columns and pylons. According to the results of the dynamic calculation, the optimal structural solution of the building frame was chosen. Simulation of wind impact is performed according to the normative documentation and in the PC "ANSYS". Analysis of the results of the account showed that the stress-strain state of the frame elements in the second model differs from the values obtained by the regulatory recommendations. It is shown that the existing design standards require clarification of methods for determining the wind load for buildings and structures of complex geometric shape.
wind impact, parametric architecture, constructive solution, finite element method, finite element model, stress-strain state
Ветровое воздействие вносит большой вклад в напряженно-деформированное состояние конструкций зданий параметрической архитектуры и требует более детального учета ветровой нагрузки , чем в нормативных документах [1].
С целью снижения ветровых воздействий на поверхности здания необходимо выбрать оптимальную конструктивную модель, отвечающую требованиям по несущей способности и соответствующую параметрической форме объекта [2].
Для исследования ветрового воздействия выбрано проектируемое двадцатиэтажное здание параметрической архитектуры административного назначения в г. Ростове-на-Дону.
Численный эксперимент по регулированию напряженно-деформированного состояния плит перекрытий каркаса здания с консольными свесами позволил определить изгибающие моменты, возникающие в зонах пересечения консольного вылета плиты перекрытия и вертикальных несущих элементов, которые необходимо учитывать при конструировании данного узла.
Разработано два варианта конструктивного решения плиты перекрытия - безбалочное (рис. 1а) и с балками (рис. 1б).
Рис.1. Конструктивное решение плиты: а) без балок; б) с балками
При моделировании эксцентриситета стержни сшиваются при помощи абсолютно жестких вставок с узлами конечно-элементной модели плиты. На рис. 2а представлена визуализации балки в виде конечно-элементной сетки. 3D модель фрагмента каркаса здания представлена на рис. 2б.
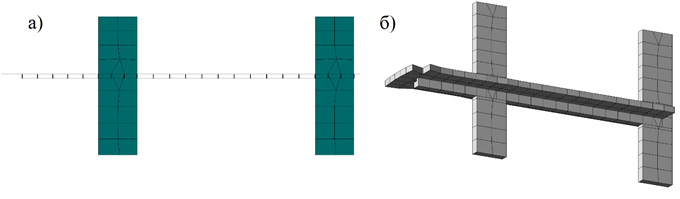
Рис.2. Визуализация балки: а) КЭ сетка; б) 3D модель
В расчетной модели учтены собственный вес, постоянные и полезные нагрузки. По результатам статического расчета получены перемещения плиты перекрытия, изолинии которых показаны на рис. 3.
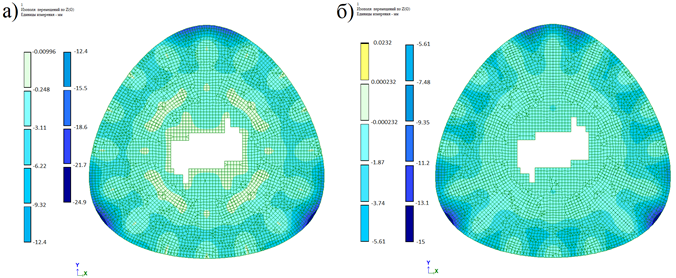
Рис.3. Вертикальные перемещения плиты перекрытия:
а) безбалочной; б) с балками
Максимальные перемещения плиты в первом варианте составляют 24,9 мм, во втором - 15 мм. В качестве ограждающих конструкций предлагается витраж алюминиевый, для которого номеруются значения вертикальных перемещений крайней точки консольного свеса. В связи с этим оптимальной признана вторая конструктивная схема.
Для исследования динамических характеристик разработаны конечно-элементные модели каркаса здания с несущими элементами в виде колон и пилонов в ПК САПФИР и импортированы в ПК ЛИРА САПР [2].
Первая модель: несущие элементы каркаса здания выполнены из бетона класса В25; и включают фундаментную плиту 1500 мм, стены подвала 400 мм, диафрагмы жесткости 250 мм, стены ядра жестокости 300 мм, плиты перекрытия 220 мм, лестничные марши и промежуточные площадки 200 мм, монолитные балки 300х400(h) мм, пилоны в подвале и на 1-4 этажах 1200х500 мм, на 5-7 этажах 1200х400 мм, выше 7 этажа 1200х500 (рис. 4).
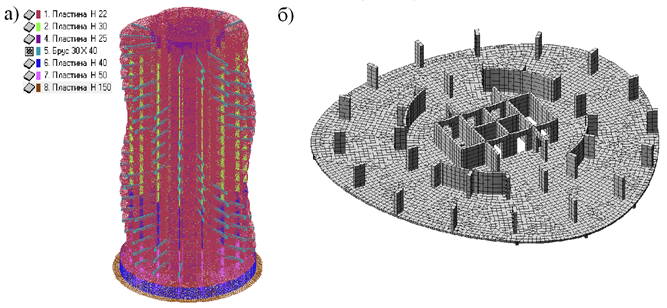
Рис.4. Первая расчетная модель:
а) распределение материалов; б) фрагмент этажа
Вторая модель отличается наличием несущих элементов в виде колонн в подвале и на 1-5 этажах сечением 600х600 мм, в 6-9 этажах – 500х500, выше 9 этажа – 400х400 (рис.5).
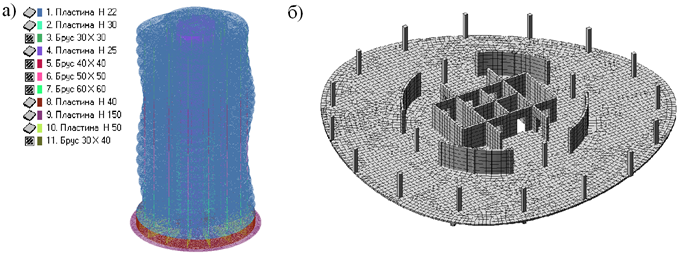
Рис.5. Вторая расчетная модель:
а) распределение материалов; б) фрагмент этажа
В расчетных моделях учтены 8 статических загружений: собственный вес несущих конструкций; постоянные нагрузки; временная (полезная) нагрузка; временная (длительная) нагрузка; постоянная нагрузка от витража и грунта; временная (снеговая) нагрузка; статический ветер по Х; статический ветер по Y.
Для исследования динамических характеристик каркаса здания выполнен модельный анализ, цель которого сводится к определению частот и форм свободных колебаний конечно-элементной модели в заданном диапазоне [3]. Наибольший интерес представляют значения первых (низших) частот свободных колебаний 
. Соответствующие формы свободных колебаний дают представление о возможных способах деформирования конструкции. На этапе проектирования модальный анализ оценивает эффективность несущего каркаса сооружения, уточняет принятые значения геометрических и физических констант, выполняет проверку на резонанс [4]. Результаты модального анализа представлены в таблице 1.
Таблица 1. Частоты и периоды колебаний (сделать на 10)
|
№ формы |
Первый вариант расчетной модели |
Второй вариант расчетной модели |
||||
|
Частота, рад/с |
Частота, Гц |
Периоды, с |
Частота, рад/с |
Частота, Гц |
Периоды, с |
|
|
1 |
3.46 |
0.55 |
1.8155 |
2.78 |
0.44 |
2.2558 |
|
2 |
3.53 |
0.56 |
1.7814 |
3.11 |
0.50 |
2.0192 |
|
3 |
3.82 |
0.61 |
1.6455 |
3.48 |
0.55 |
1.8065 |
|
4 |
11.74 |
1.87 |
0.5350 |
8.41 |
1.34 |
0.7464 |
|
5 |
14.29 |
2.28 |
0.4395 |
12.49 |
1.99 |
0.5027 |
|
6 |
14.90 |
2.37 |
0.4214 |
13.19 |
2.10 |
0.4762 |
|
7 |
23.62 |
3.76 |
0.2659 |
14.75 |
2.35 |
0.4256 |
|
8 |
25.29 |
4.03 |
0.2483 |
21.47 |
3.42 |
0.2924 |
|
9 |
25.85 |
4.12 |
0.2429 |
24.16 |
3.85 |
0.2599 |
|
10 |
25.87 |
4.12 |
0.2427 |
24.53 |
3.91 |
0.2560 |
Первая форма колебаний каркаса здания для двух расчетных моделей приведена на рис. 6.
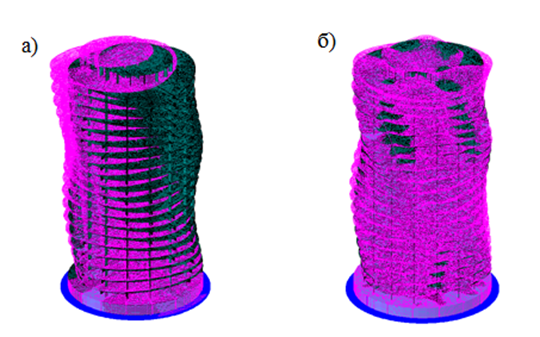
Рис. 6. Первая форма собственных колебаний каркаса здания:
а) первая расчетная модель; б) вторая расчетная модель
Анализ результатов динамического расчета показал, что первая форма колебаний в первой модели поступательная, во второй - крутильная. Процент вклада модальных масс составил для первой модели 13,4 %, для второй 0%. Характер форм колебаний второй модели показывает недостатки принятых конструктивных решений. Для дальнейших исследований ветрового воздействия принята первая модель с простыми конструктивными решениями по каркасу здания [5].
При расчете пульсационной составляющей ветровой нагрузки необходимо учесть первые 3 формы колебаний, значения частот которых меньше предельных 
Расчет пульсационной нагрузки выполнен по двум методам: на основе нормативных значений, указанных в СП «Нагрузки и воздействия» и при учете действительных значений, полученных по результатам расчета в ПК «ANSYS» [6].
В результате расчета с учетом пульсации ветра, рассчитанной по первому методу, получены перемещения несущих конструкций каркаса здания (рис. 7). Максимальные горизонтальные перемещения составляют вдоль оси X 19,1 мм; вдоль оси Y 20,1 мм, что меньше нормативных значений.
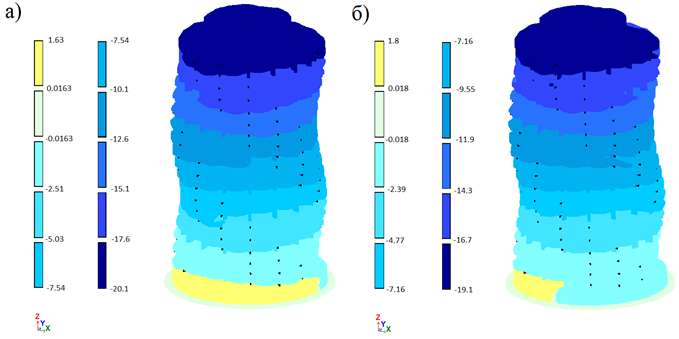
Рис. 7. Перемещения от нормативной ветровой нагрузки:
а) вдоль оси Y; б) вдоль оси X
Выполнено моделирование ветрового воздействия в ПК «ANSYS» для уточнения ветрового давления и зон комфортности здания параметрической формой.
Максимальные горизонтальные перемещения составляют вдоль оси X 30,7 мм; вдоль оси Y 33,1 мм, что меньше нормативных значений (рис.8.).
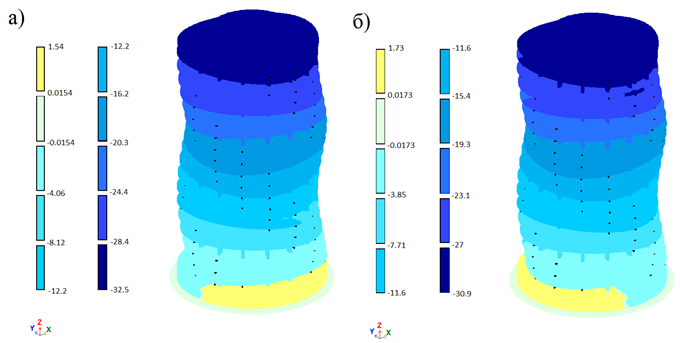
Рис. 8. Перемещения от расчетной ветровой нагрузки:
а) вдоль оси Y; б) вдоль оси X
Моделирование ветровых потоков в ПК ANSYS Fluent позволило уточнить значения нагрузки в расчетной модели каркаса здания параметрической архитектуры. Горизонтальные перемещения увеличились на 40 % по сравнению с результатами, полученными в соответствии с нормативной документацией [7].
Анализ моделирования ветрового воздействия методом конечных элементов показал, что существующие нормы проектирования требуют уточнения методики определения ветровой нагрузки для зданий и сооружений сложной геометрической формы.
При расчете ветровой нагрузки в соответствие с СП ограничены поверхности проектируемых зданий. Объекты параметрической архитектуры сложной геометрической формы действующими нормами не рассматриваются.
Разработан следующий алгоритм расчета объекта параметрической архитектуры на ветровое воздействие:
- регулирование напряженно-деформируемого состояния элементов каркаса зданий и сооружений методом варьирования жесткостей;
- анализ динамических характеристик объекта и выбор рационального - варианта конструктивного решения каркаса здания;
- моделирование ветрового воздействия в ПК ANSYS;
- расчет пульсационной составляющей ветровой нагрузки и определение зон комфортности;
- определение напряженно-деформируемого состояния элементов каркаса здания параметрической архитектуры с учетом пульсационной составляющей ветровой нагрузки.
Предлагаемый авторами подход к расчету ветрового воздействия на объекты параметрической архитектуры позволяет проектировать оптимальные конструкции с достаточной надежностью и долговечностью.
1. Agahanov E. K., Kravchenko G. M., Osadchij E.V., Trufanova E.V. Raschet zdanij slozhnoj geometricheskoj formy na vetrovye vozdejstviya. Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki. - 2017. - № 2. - p. 8-17.
2. Agahanov E.K. O razvitii kompleksnyh metodov resheniya zadach mekhaniki deformiruemogo tverdogo tela. Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki. - 2013. - № 2. - p. 39-45.
3. Rabinovich I.M. Osnovy dinamicheskogo rascheta sooruzhenij na dejstvie mgnovennyh ili kratkovremennyh sil, M.- L., 1945. p. 17-19.
4. Zotova E.V., Panasyuk L.N. CHislennoe modelirovanie dinamicheskih sistem s bolshim chislom stepenej svobody na impulsnye vozdejstviya // Inzhenernyj vestnik Dona, 2012. № 3 URL: ivdon.ru/magazine/archive/n3y2012/933.
5. Agahanov E.K., Kravchenko G.M., Trufanova E.V. Regulirovanie parametrov sobstvennyh kolebanij prostranstvennogo karkasa zdaniya // Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki, - 2016. - № 3. - p. 8-15.
6. Gajdzhurov P.P. Metody, algoritmy i programmy rascheta sterzhnevyh sistem na ustojchivost i kolebaniya. Uchebnoe posobie. − Novocherkassk: YURGTU, 2010. 230 p.
7. Zyryanov V.V. Metody ocenki adekvatnosti rezultatov modelirovaniya // Inzhenernyj vestnik Dona, 2013. № 2 URL: ivdon.ru/magazine/archive/n2y2013/1707.ru/magazine/archive/n2y2013/1707.
