from 01.01.2019 until now
Arhangel'sk, Arkhangelsk, Russian Federation
Arhangel'sk, Arkhangelsk, Russian Federation
The use of the average values of physical and deformation characteristics for the entire extremely heterogeneous peat layer leads to mistakes in estimation a settlement of the embankments set up over it. The results of numerous oedometer tests of peat and empirical equations for calculating the void ratio of peat as a function of its initial value and the load are presented. A new approach to carrying out the geotechnical surveys in a wetland is proposed.
peat, oedometer tests, void ratio, peat compressibility, compression parameters
Торф, состоящий из остатков растений различного размера и разной степени разложения, представляет собой крайне неоднородное вещество. У образцов торфа, отобранных на различной глубине в одной скважине, и даже с одной глубины из забоя шурфа, как правило, наблюдается значительный разброс значений коэффициента пористости. Это приводит к существенным отличиям деформации образцов при компрессионных испытаниях. В качестве примера на рис.1, а дана компрессионная зависимость, полученная в свое время Н.П. Коваленко [2]. Под нагрузкой 50 кПа, создаваемой насыпью высотой около 3 м, относительные деформации исследованного торфа могут составить ε = 0,32±0,09, что при мощности слоя 5 м дает весьма значительный интервал варьирования расчетной осадки, равный 0,9 м.
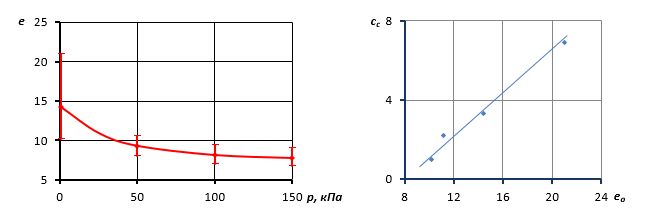
Рисунок 1. Результаты испытаний торфа в одометре [2]:
а – компрессионная зависимость, б - зависимость индекса компрессии
от начального коэффициента пористости
Несмотря на столь существенные отличия по сжимаемости, слой торфа обычно принимают за один инженерно-геологический элемент со средними значениями характеристик, так как его деление на несколько элементов ведет к соответствующему росту затрат на лабораторные исследования. Сказанное особенно значимо для одометрических испытаний торфа, продолжительность которых может достигать нескольких месяцев.
Необходимо заметить, что для исключения погрешностей, связанных с линейной аппроксимацией компрессионной зависимости, в расчете осадки торфа в основании земляного полотна автомобильных дорог модуль деформации обычно не используют. Деформации торфа определяют прямо по компрессионной кривой или вычисляют с помощью различных эмпирических зависимостей [5].
Авторы предлагают следующий порядок исследования торфяной залежи при изысканиях:
1. При проходке скважин выполнять отбор проб торфа на влажность с шагом около 0,5 м. Слой торфа, принятый за один инженерно-геологический элемент (ИГЭ), разделить по глубине и в плане на расчетные геологические элементы (РГЭ) с примерно одинаковыми значениями влажности (рис.2).
2. Образцы ненарушенной структуры (монолиты), предназначенные для испытаний на сжимаемость, отбирать в соответствии с нормативными документами – не менее 6 штук из всего инженерно-геологического элемента. Данные лабораторных испытаний образцов представлять не в виде средних (нормативных) характеристик сжимаемости, а эмпирическими зависимостями коэффициента пористости e от его начального значения e0 и нагрузки p.
3. Используя значения влажности, а также полученные при испытаниях образцов-монолитов средние значения плотности частиц и коэффициента водонасыщения, вычислить коэффициент пористости торфа в каждом из РГЭ. Заметим, что плотность частиц торфа варьирует в очень узком интервале, а коэффициент водонасыщения неосвоенной залежи близок к единице.
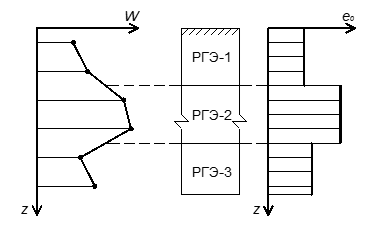
Рисунок 2. Выделение расчетных геологических элементов в слое торфа
Наличие указанных данных в отчете по изысканиям позволит находить осадку торфа в основании сооружения как сумму деформаций отдельных РГЭ, вычислять которые следует с использованием эмпирических зависимостей e = f(e0, p). Реализация всех пунктов приведенного алгоритма изучения торфяной залежи, кроме поиска эмпирических зависимостей, не вызывает затруднений. Различными авторами для этого использовались степенные, экспоненциальные функции [3, 9]. Применение таких нелинейных зависимостей вызывает определенные неудобства, кроме того, связано с необходимостью индивидуального подбора коэффициентов для каждой из экспериментальных компрессионных кривых.
Зарубежные авторы выявили наличие линейной зависимости между индексом компрессии торфа, вычисляемым по формуле сс = Δe/(lg p2 – lg p1), и начальным коэффициентом пористости или влажностью [7, 8, 10]. Обработка данных Н.П. Коваленко [2] показала, что, действительно, зависимость cc = f(e0) является линейной (рис. 1,б). Между тем оказалось, что применение логарифмической шкалы р для расчета компрессионной кривой вызывает затруднения из-за неопределенности начальной нагрузки р1. Сказанное относится и к расчету осадки водонасыщенного слоя торфа, где напряжения от собственного веса весьма незначительны.
К сожалению, из-за неполного представления характеристик всех испытанных образцов воспользоваться приводимыми в литературе экспериментальными данными для выявления требуемых зависимостей не представляется возможным.
В настоящей статье представлены результаты экспериментов, целью которых был поиск удобной для практического применения зависимости e = f(e0, p).
Испытывались образцы, отобранные главным образом на неосвоенных неосушенных болотах в окрестностях г. Архангельска с глубины не менее 0,5 м. Степень разложения торфа составляла 25-45 %, плотность - 0,98–1,12 г/см3, плотность частиц – 1,44-1,48 г/см3. Использовались также данные исследований, выполненных ранее на кафедре [4]. Эксперименты проводили в компрессионно-фильтрационных приборах на образцах ненарушенной структуры с площадью поперечного сечения 60 см2. Большинство образцов имели высоту 70 мм, отдельные – 50 мм. Приборы размещали в помещении с температурой 5–12°С, что замедляло разложение органического вещества торфа.
На первом этапе исследований были проведены испытания образцов под нагрузкой 50 кПа. Сокращение продолжительности экспериментов достигалось приложением нагрузки в одну ступень. При последовательном – ступенчатом - наращивании нагрузки продолжительность испытаний возрастала бы в несколько раз. Заметим, что ранее нами было установлено, что конечные деформации торфа при двух способах загрузки образцов практически не отличаются [4]. Опыты продолжались не менее 3 недель – до так называемой условной стабилизации, когда деформации образцов не превышали 0,01 мм/сут.
Обработка результатов опытов показала, что зависимость достигаемого в одометре под постоянной нагрузкой коэффициента пористости е от его исходного значения е0 может быть принята линейной (коэффициент детерминации R2 = 0,78) (рис. 3):
e = ke0 + b, (1)
где k= 0,27, b= 3,8.
Заметим, что в массив данных включены еще и результаты испытаний образцов, отобранных из-под насыпи. Их начальный коэффициент пористости не превышал 9,4. Соответствующие точки выделены на рисунке 3.
Аналогичная зависимость при p = const была получена E. Dhianty и I.B. Mochtar для глинистых грунтов [6].
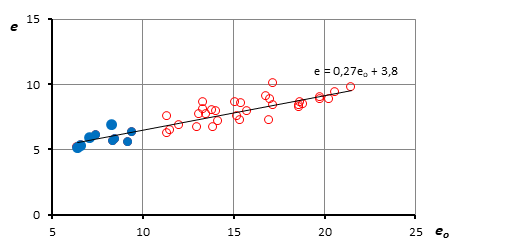
Рисунок 3. Зависимость e от e0 при p = 50 кПа
Вполне очевидно, что применимость зависимости (1) ограничивается областью e0>e' , где е' - координаты точки пересечения полученной зависимости с прямой е = е0, соответствующей отсутствию деформаций образца (рис. 4). Значение е' можно найти из уравнения (1), подставив в него е' вместо е и е0:
e' = b/(1 - k). (2)
В частности, в рассматриваемом случае при р = 50 кПа е' = 5,21.
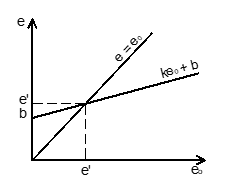
Рисунок 4. Схема к определению e'
После простейших преобразований зависимость (1) приводится к следующему виду (рис. 5):
е = k(e0 – e') + e'. (3)
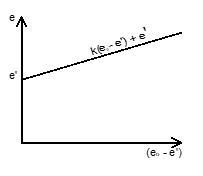
Рисунок 5. Зависимость e от (e0 - e')
Далее компрессионные испытания торфа проводили по стандартной методике при ступенчатом наращивании нагрузки (12,5; 25; 50 и 100 кПа), но на меньшем числе образцов. Результаты обработки экспериментальных данных представлены в итоговой таблице 1. Как видим, при всех значениях р зависимость е = f(e0) оказалась линейной при достаточно высоких значениях коэффициента детерминации R2.
Таблица 1. Параметры эмпирических зависимостей сжимаемости торфа
|
р, кПа |
k |
b |
e' |
R2 |
|
12,5 |
0,46 |
6,3 |
11,67 |
0,74 |
|
25 |
0,34 |
5,5 |
8,33 |
0,67 |
|
50 |
0,27 |
3,8 |
5,21 |
0,78 |
|
100 |
0,16 |
3,4 |
4,05 |
0,58 |
Анализ полученных данных показал, что коэффициент k и коэффициент пористости e' находятся в степенной зависимости от нагрузки: k = αpm и e'=βpm. Для исследованного торфа показатель степени m оказался равным -0,5, отсюда приведенные формулы могут быть записаны в следующем виде:

где α= 1,60 кПа0,5; β= 42,77 кПа0,5.
Для обеих зависимостей R2 = 0,91. Соответствующие графики показаны на рис.6.
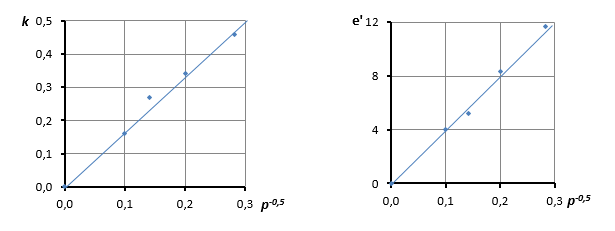
Рисунок 6. Зависимость k и e' от рm
В таблице 2 в качестве примера применимости полученных уравнений приведены расчетные и экспериментальные значения компрессионной зависимости одного из образцов торфа с начальным коэффициентом пористости eo=13,5. Как видим, расчет дал вполне приемлемую погрешность.
Таблица 2. Расчетные и экспериментальные значения коэффициента пористости
|
p, кПа |
20 |
40 |
80 |
160 |
|
р-0,5, кПа-0,5 |
0,22 |
0,16 |
0,11 |
0,08 |
|
e’ |
9,4 |
6,8 |
4,7 |
3,4 |
|
eрасч |
10,8 |
8,5 |
6,2 |
4,6 |
|
eэксп |
10,3 |
8,3 |
6,0 |
4,6 |
Конечно, коэффициенты α, β и показатель степени m для других типов торфа могут отличаться от значений, полученных нами. Их легко определить экспериментально, проведя стандартные компрессионные испытания, причем для сокращения продолжительности испытаний образцы можно загружать лишь 2-3 ступенями нагрузки, например, 25, 50 и100 кПа.
Тем не менее, нами сделана попытка расчета деформаций водонасыщенных образцов, подвергавшихся длительным испытаниям в экспериментальных исследованиях В.Н. Бронина [1]. В уравнение (4) задавались полученные нами значения коэффициентов α и β. Из таблицы 3 видно, что кроме образца, испытанного при р = 10 кПа, экспериментальные и расчетные деформации имеют близкие значения. Отличия на начальном участке компрессионной зависимости могут быть обусловлены особенностями проведения испытаний при небольшой нагрузке.
Таблица 3. Расчет деформаций образцов по литературным данным [1]
|
p, кПа |
Коэффициент пористости |
Относительные деформации |
||
|
eo |
eрасч |
εрасч |
εэксп |
|
|
10 |
20,8 |
17,3 |
0,16 |
0,10 |
|
20 |
18,9 |
12,9 |
0,30 |
0,25 |
|
40 |
18,4 |
9,7 |
0,45 |
0,42 |
|
80 |
16,9 |
7,0 |
0,55 |
0,57 |
|
160 |
16,5 |
5,0 |
0,66 |
0,65 |
Выводы:
1. При инженерно-геологических изысканиях торфяную залежь следует делить на расчетные геологические элементы с примерно одинаковыми значениями влажности и коэффициента пористости, а данные компрессионных испытаний представлять не в виде средних характеристик сжимаемости, а эмпирическими зависимостями коэффициента пористости от его начальных значений и нагрузки.
2. Экспериментально установлено, что зависимость достигаемого в одометре под постоянной нагрузкой коэффициента пористости е от его исходного значения е0 может быть принята линейной: е = k(e0 – e') + e', где k = αpm и e'=βpm.
1. Bronin V.N. Prognoz skorosti deformacii torfyanyh gruntov v sluchae odnomernoy zadachi/ Avtoreferat diss. na soisk. uch. st. kand. tehn. nauk. Leningrad: LISI, 1973. 25 s.
2. Kovalenko N.P., Hudyakov A.D., Gorelikov V.S. Predpostroechnoe uplotnenie torfyanoy zalezhi. Arhangel'sk: Severo-zapadnoe knizhnoe izdatel'stvo, 1971. 96 s.
3. Morareskul N.N. Osnovaniya i fundamenty v torfyanyh gruntah. Leningrad: Stroyizdat, 1979. 80 s.
4. Nevzorov A.L., Nikitin A.V., Zaruchevnyh A.V. Gorod na bolote. Arhangel'sk: IPC SAFU, 2012. 157 s.
5. Posobie po proektirovaniyu zemlyanogo polotna avtomobil'nyh dorog na slabyh gruntah. M.: Mintrans RF, 2004. 155 s.
6. Dhianty E., Mochtar I.B. Method of removing secondary compression on clay using preloading. MATEC Web of Conferences, 195, 03006, ICRMCE, 2018. 10 p. DOI:https://doi.org/10.1051/matecconf/201819503006.
7. Engineering and design settlement analysis/ Eng. Manual No. 1110-1-1904. Washington: US Army Corps of Eng. 1990. 205 p.
8. Gruen H.A., Lovell C.W. Use of peats as embankment foundations, JHRP-83/3, Purdue Univ. West Lafayette, Indiana, 1983. 149 p.
9. Koster K., De Lange G.D., Harting R., De Heer E., Middelkoop H. Characterizing void ratio and compressibility of Holocene peat with CPT for assessing coastal-deltaic subsidence. Quarterly J. of Eng. Geology and Hydrogeology. 2018. DOI:https://doi.org/10.1144/qjegh2017-120
10. Mesri G., Ajlouni M. Engineering properties of fibrous peats. J. of Geotechnical and Geoenvironmental Eng., July 2007. p. 850-866. DOI:https://doi.org/10.1061/(ASCE)1090-0241(2007)133:7(850).


















