Russian Federation
Russian Federation
Russian Federation
Russian Federation
UDC 539.376
As a mathematical tool for modeling the process of continuous deformation of reinforced con-crete structures, the finite element method was used in combination with a step-by-step proce-dure for numerical integration according to the time coordinate of the resulting operator-matrix equation. The program code is implemented on the basis of the Microsoft Visual Studio compu-ting platform and the Intel Parallel Studio XE compiler with the built-in Intel Visual Fortran Com-poser XE text editor. The processes of storing and processing working arrays are imple-mented in terms of sparse matrices. The descriptive graphics of the Matlab computer system were used to visualize the calculation results. All computational experiments were performed using the authorized Polygon complex. The objectives of the study include assessing the accuracy of the proposed methodology for analyzing the long-term deformation of reinforced concrete structures under various methods of external force action.
finite element method, creep of concrete, reinforced concrete girder structures
Введение
В настоящее время проектирование многоэтажных и высотных зданий из монолитного железобетона базируется на рамно-связевой конструкционной схеме, позволяющей в известной степени обеспечить «живучесть» здания в случае прогрессирующего (лавинообразного) разрушения. Расчет на прочность строительных конструкций из монолитного железобетона базируется на применении метода конечных элементов (МКЭ) в форме метода перемещений. Общеизвестно, что данный подход может быть использован для математического моделирования широкого круга задач статики и динамики, включая решения с учетом геометрической и физической нелинейностей. Однако, не смотря на мультифизичность таких лидирующих автоматизированных программных комплексов, как ANSYS и ABAQUS, они не позволяют исследовать поведение изгибаемых железобетонных конструкций при длительном деформировании с использованием наследственных функций ползучести бетона [1]. Это обуславливает актуальность проблемы разработки методики конечно-элементного моделирования, реализующей механико-математическую модель упруго-ползучего тела, позволяющую учитывать эффект быстро нарастающей ползучести бетона в момент приложения эксплуатационной нагрузки.
Объекты и методы исследования
В МКЭ в форме метода перемещений зависимость между напряжениями и деформациями записываем в форме закона релаксации
$$\sigma(t)=E(t)
\left[\varepsilon(t)-\int_{\tau_0}^tU(t,\tau)\varepsilon(\tau)dT\right],$$
где U(t,τ) — мера релаксации. В дальнейшем считаем, что функция U(t,τ) имеет структуру аналогичную функции меры ползучести C(t,τ) [1]. Такой подход позволяет при конечно-элементном моделировании воспользоваться экспериментальными данными, полученными в опытах на ползучесть. Процесс релаксации при одноосном деформировании описываем интегральным уравнением
$$\sigma(t)=\sigma_k\left[1+E(t)\int_{\tau_0}^tPi(t,\tau)dT\right],$$
где σk=const — заданная величина напряжения; $$\Pi(t,\tau)=-\frac{\delta}{\delta\tau}\left[\frac{1}{E(\tau)}+C(t,\tau)\right]$$ — ядро ползучести.
Для моделирования длительного деформирования дополнительно введем модифицированный вектор-столбец узловых перемещений [2]
$$\{\tilde{q}(t)\}=(1-R)\{q\}$$(1)
Тогда вектор-столбец перемещений в произвольной точке КЭ определяем по формуле
$$\{\tilde{u}\}=(1-R)[\def\MYF{\mathop{\rm F}\limits}
\MYF_{3\times n_r}]\{q\},$$
где [F] — матрица, «функций формы» КЭ; интегральный оператор $$R\varepsilon_{ij}=\int_{\tau}^t R(t,\tau)\varepsilon_{ij}(\tau)d\tau,$$ в котором R(t,τ) — наследственная функция.
Материал КЭ считаем изотропным линейно вязкоупругим. Уравнение состояния в общем случае представим в форме
$$\{\sigma\}=[D_0][\def\MY\Phi{\mathop{\rm \Phi}\limits}
\MY\Phi_{6\times n_r}]\{\tilde\sigma\}+[D_1][\def\MY\Phi{\mathop{\rm \Phi}\limits}
\MY\Phi_{6\times n_r}]\{\tilde\sigma\},$$ (2)
здесь [Ф] — матрица, устанавливающая связь между узловыми перемещениями и деформациями; матрицы упругости, соответствующие объемной D0 и сдвиговой D1 деформациям.
Результирующее матричное уравнение МКЭ запишем в виде
$$([k_0]+[K_1])\{\tilde q\}-\{P(t)\}=0,$$(3)
где матрицы жесткости КЭ, учитывающие объемную и сдвиговую деформации
$$[k_0]=\int_{v_e}[\Phi]^T[D_0][\Phi]dv;$$ $$[k_1]=\int_{v_e}[\Phi]^T[D_1][\Phi]dv;$$
{P(t)} — вектор-столбец узловых сил, учитывающий квазистатический характер нагружения.
Подставив в уравнение (3) зависимость (1), получим
$$([k]-[k_0]R_0-[k_1]R_c)\{q\}-\{P(t)\}=0,$$ (4)
где $$[k]-[k_0]+[k_1]=\int_{v_e}[\Phi]^T[D][\Phi]dv;$$ [D]=[D0]+[Dc]; R0, Rc — наследственные функции, соответствующие объемной и сдвиговой длительной деформации.
Для вычисления интеграла $$R_a\{q\}=\int_0^tR_{\alpha}(t,\tau)\{q(\tau)\}d\tau, \alpha=0,c$$ воспользуемся численным методом, основанном на формуле трапеций. Разбив временной интервал [0, t] на m равноотстоящих временных узловых точек так, чтобы t=mΔt, запишем рекуррентные соотношения в виде:
$$R_a\{q\}\approx R_{\alpha}(m\Delta t)\{q^0\}\frac{\Delta t}{2}+\sum^{m-j}_{j=1}R_{\alpha}((m-j)\Delta t)\{q^j\}\Delta t+R_{\alpha}(0)\{q^m\}\frac{\Delta t}{2},$$ (5)
где Δt — шаг интегрирования.
С учетом выражения (5) матричное уравнение (4) принимает вид$$[k]\{q^m\}-[k_0]\left\{
R_0(m\Delta t)\{q^0\}\frac{\Delta t}{2}+\sum^{m-1}_{j-1}R_0((m-j)\Delta t)\{q^j\}\Delta t+R_0(0)\{q^m\}\frac{\Delta t}{2}
\right\}-$$
$$-[k_1] \left\{
R_c(m\Delta t)\{q^0\}\frac{\Delta t}{2}+\sum^{m-1}_{j-1}R_c((m-j)\Delta t)\{q^j\}\Delta t+R_c(0)\{q^m\}\frac{\Delta t}{2}
\right\}-{P}=0.$$
Или в компактной форме
$$[k^0]\{q^m\}=\{P\}+[k^m]\{q^0\}+\sum^{m-1}_{j-1}[k^j]\{q^j\},$$ (6)
здесь введены обозначения:
$$[k^0]=[k]-[k_1]R_0(0)\frac{\Delta t}{2}-[k_1]R_c(0)\frac{\Delta t}{2};$$
$$[k^m]=[k_0]R_0(0)(m\Delta t)\frac{\Delta t}{2}+[k_1]R_c(m\Delta t)\frac{\Delta t}{2};$$
$$[k^j_1]=[k_0]R_0((m-j)\Delta t)\Delta t+[k_1]R_c((m-j)\Delta t)\Delta t)\Delta t.$$
Соотношения (6) могут быть легко запрограммированы.
Процедура вычисления напряжений в КЭ основана следующем выражении:
$$\{\sigma\}=\{[D][\Phi]-[D_0][\Phi]R_0-[D_1][\Phi]R_c\}\{q\}.$$
В развернутом виде данная зависимость принимает форму
$$\{\sigma\}=[D][\Phi]\{q^m\}-[D_0][\Phi]\left\{R_0(m\Delta t)\{q^0\}\frac{\Delta t}{2}+\sum^{m-1}_{j-1}R_0((m-j)\Delta t)\{q^j\}\Delta t+R_0(0)\{q^m\}\frac{\Delta t}{2}\right\}-$$
$$-[D_1][\Phi]\left\{R_c(m\Delta t)\{q^0\}\frac{\Delta t}{2}+\sum^{m-1}_{j-1}R_c((m-j)\Delta t)\{q^j\}\Delta t+R_c(0)\{q^m\}\frac{\Delta t}{2}\right\}.$$
Рабочие массивы, предназначенные для хранения промежуточной информации о предыстории нагружения конструкции, хранятся в виде временных наборов последовательного доступа во внешней памяти. Представленные зависимости легли в основу авторизированного учебно-исследовательского программного комплекса Polygon [3].
Выполнены вычислительные эксперименты численного интегрирования с применением равномерной дискретизации временной оси, а также при выборе шага по времени на основании арифметической и геометрической прогрессий. Установлено, что наилучшее приближение к точному решению дает равномерная схема численного интегрирования с постоянным шагом [2].
Результаты исследований
Для демонстрации возможностей разработанного математического и программного обеспечения рассмотрим конкретные числовые примеры.
Пример 1. Расчет напряженно-деформированного состояния железобетонной плиты квадратной в плане на продавливание
В лаборатории McNeice лондонского университета в 1967 году [4] были проведены испытания на продавливание квадратной железобетонной плиты с размерами 914,4 мм (36 дюймов) × 914,4 мм (36 дюймов) и толщиной 44,45 мм (1,75 дюйма). Плита имела угловые опирания и была усилена арматурной сеткой в двух ортогональных направлениях на глубине 33,3 мм (1,31 дюйма). Фотография экспериментального стенда представлена на рис. 1.
В натурном эксперименте плита располагалась вертикально для исключения влияния собственного веса конструкции и удобства размещения измерительной аппаратуры.
Данные экспериментальные исследования широко используются разработчиками программного обеспечения для проверки и валидации численных моделей и методов прочностного анализа железобетонных конструкций [5, 6, 7].
На рис. 2 приведена конструкционная схема плиты с указанием размеров в миллиметрах. По углам плиты расположены опоры из стали 76,2x76,2 мм.
С учетом симметрии рассмотрим ¼ часть плиты. Конечно-элементные модели монолитной бетонной части плиты и армирующей сетки показаны на рис. 3.

Рис. 1. Стенд для испытания квадратной в плане плиты на продавливание [4]
Для установления соответствия физического и компьютерного экспериментов в местах опор и приложения нагрузки также предусматриваем размещение стальных пластин толщиной 10 мм.
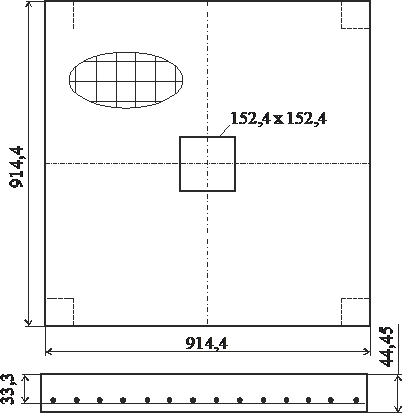
Рис. 2. Схема плиты [119]
Механические константы бетона: Ec= 2,86·1010 Н/м2; v_c = 0,15; Rb = 30 МПа; Rbt = 2,9 МПа. Арматура – стальной пруток диаметром 6 мм с шагом армирования 100x100 мм. Механические константы арматуры: E= 2·1011 Н/м2; v =0,28. Собственный вес плиты не учитываем.

Рис. 3. Конечно-элементные модели плиты и арматурной сетки
По аналогии с экспериментом в центре плиты прикладываем сосредоточенную силу F = 7,5 кН. С учетом симметрии на ¼ часть – F1/4 = 1,875 кН.
Результаты конечно-элементного моделирования в виде картин распределения прогибов uz, полученные с помощью расчетно-вычислительных комплексов ANSYS, Polygon и DIANA для ¼ части плиты представлены на рис. 4–6. Во всех случаях применялись объемные и стержневые КЭ одинакового порядка. Как видно из рис. 4 и 5 значения прогибов в центре пластины практически совпадают:
uz max= –0,266·10–3 м (ANSYS); uz max= –0,276·10–3 м (Polygon).
Вместе с тем прогиб, полученный с использованием комплекса DIANA uz max= –1,45·10-3 м существенно превышает результаты комплексов ANSYS и Polygon. Отметим, что вычисления на базе комплексов ANSYS и Polygon выполнялись с использованием линейно упругой модели материала плиты. Известно лишь, что в комплексе DIANA для расчета плиты реализован шаговый алгоритм нагружения. Подчеркнем, что результат вычислительного эксперимента DIANA [8] хорошо согласуется с экспериментальными данными [9, 10].
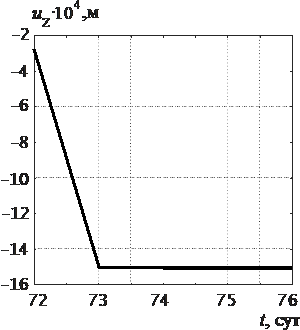
Выполним расчет плиты с учетом эффекта быстро нарастающей ползучести бетона. Здесь и далее параметры наследственной функции принимаем в соответствии рекомендациями С.В. Александровского [1]. Назначим момент времени приложения нагрузки равным 72 сут. Полученный в такой постановке график зависимости прогиба в центре плиты от временной координаты uz∼t приведен на рис. 7.
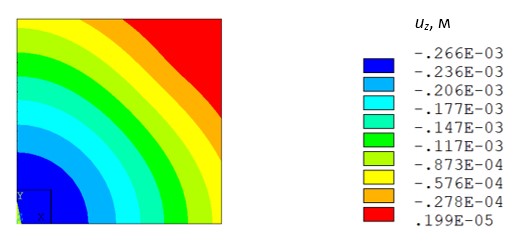
Рис. 4. Визуализация распределения поля uz (ANSYS)
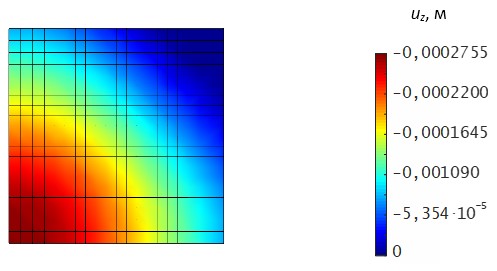
Рис. 5. Визуализация распределения поля uz (Polygon)
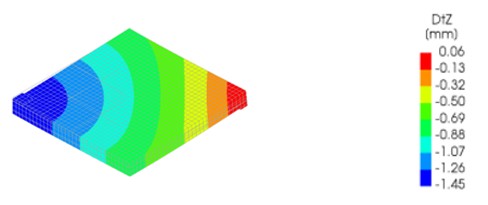
Рис. 6. Визуализация распределения поля uz (DIANA) [8]
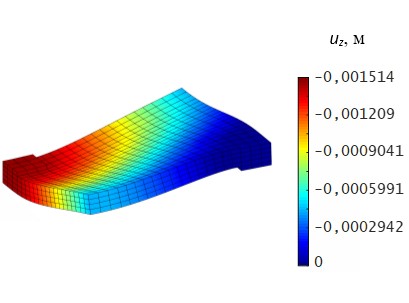
Из приведенного графика следует, что включение в расчетную модель учета ползучести позволяет получить решение (uz= –1,51·10-3 м) хорошо согласующееся с данными эксперимента [4]. Визуализация соответствующей картины перемещений для момента времени 76 сут приведена на рис. 8.
Относительная погрешность при использовании комплекса Polygon с учетом ползучести бетона составляет 4%.
|
|
|
|
|
Рис. 7. График прогиб uz∼t с учетом |
Рис. 8. Картина распределения вертикальных перемещений |
|
Из рассмотренного примера следует вывод о том, что ключевую роль при отработке методики расчета железобетонных конструкций с учетом нелинейной деформации бетона играет настройка параметров комплекса Polygon.
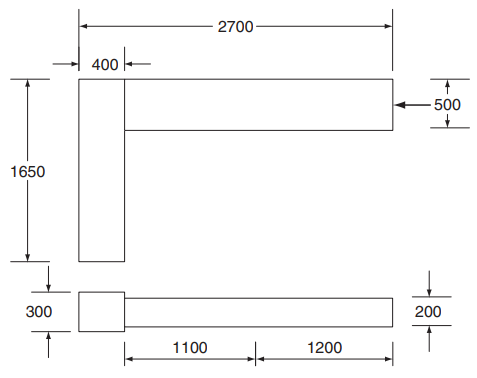
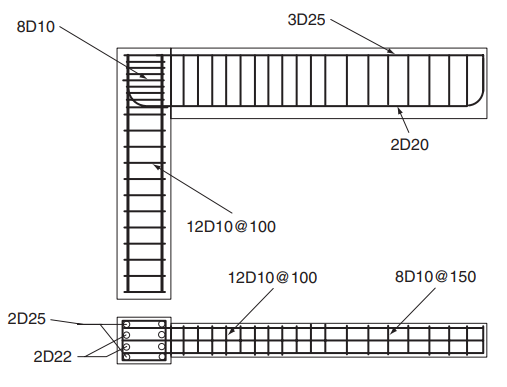
Пример 2. Анализ несущей способности узла железобетонной портальной рамы. В настоящее время при строительстве многоэтажных и многопролетных зданий из монолитного железобетона широко используются конструктивные решения, базирующиеся на применении портальных рам. Поэтому представляет определенный интерес выполнить прочностной расчет узла портальной рамы, воспринимающего горизонтальное усилие, приложенное к свободному торцу ригеля. Основные размеры и схема армирования узла портальной рамы показаны на рис. 9 и 10. Данные для расчета взяты из [10].
|
Рис. 9. Размеры в мм |
Рис. 10. Схема армирования [11] |
Расчетная схема узла приведена на рис. 11.

Рис. 11. Расчетная схема узла портальной рамы [11]
Механические константы материалов:
- бетон Eб = 3·1010 Н/м2; vб = 0,2; Rb= 34,2 МПа; Rbt = 2,65 МПа.
- арматура (сталь) E = 2·1011 Н/м2; v =0,28.
Как и в примере 2 для конечно-элементного моделирования данной конструкции используем объемные восьмиузловые и стержневые балочные КЭ (рис. 12).
С целью верификации предварительно выполним расчет узла с помощью комплексов ANSYS и Polygon. При этом используем одинаковые конечно-элементные модели. Для моделирования бетона в ANSYS используем КЭ типа SOLID185. Значение сосредоточенной силы F = 50 кН, прикладываем к площадке толщиной 0,015 м, расположенной на свободном торце ригеля. Материал данной площадки — сталь.
Визуализация полей перемещений ux в направлении действия силы представлена на рис. 13 и 14.
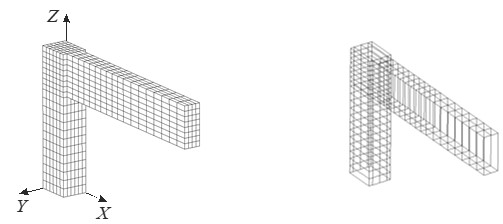
Рис.12. Конечно-элементные модели массива и армирующего каркаса
узла портальной рамы
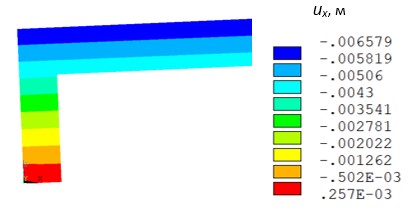
Рис. 13. Картина распределения поля ux (ANSYS)
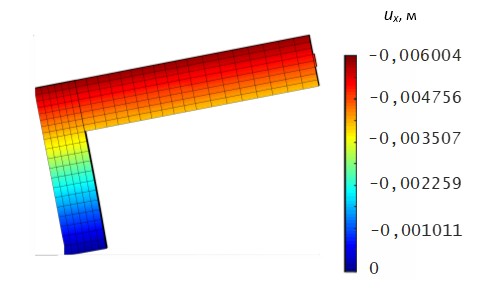
Рис. 14. Картина распределения поля ux (Polygon)
Как видно значение максимального смещения на рис. 13 во втором знаке отличается в большую сторону от аналогичной величины на рис. 14. При количественной оценке данного рассогласования устанавливаем, что модель комплекса Polygon на 10% завышает жесткость рассматриваемой конструкции в направлении оси. Вместе с тем, если в ANSYS бетон моделировать объемными элементами SOLID65 с активированными дополнительными степенями свободы, то получаем |ux max|= 0,006102 м, что практически совпадает с результатом комплекса Polygon. В случае деактивации функции дополнительных степеней свободы имеем |ux max|= 0,005645 м. Отметим, что КЭ типа SOLID65 разработаны специально для моделирования железобетонных конструкций.
Картины распределения сдвиговых напряжений ϭx, возникающих в плоскости X0Z, в зонах примыкания к узлу рамы, полученные с помощью комплексов ANSYS и Polygon, приведены на рис. 15 и 16.
Сравнивая результаты расчетов, заключаем, что оба комплекса позволяют качественно выявить область концентрации напряжений ϭx в угловой зоне узла портальной рамы. Значения максимальных касательных напряжений в этом месте, определенные двумя способами, достаточно близки:
ϭx max= 0,212 МПа (ANSYS SOLID185); ϭx max= 0,162 МПа (ANSYS SOLID65);
|ϭx max|= 0,1978 МПа (Polygon).

Рис. 15. Распределение напряжений ϭx в узле (ANSYS)
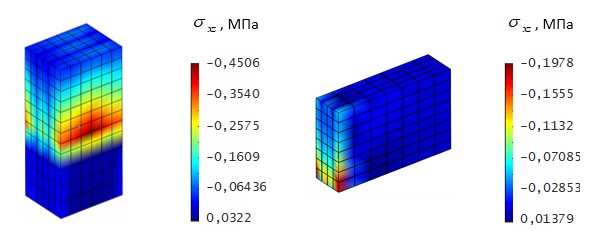
Рис. 16. Распределение напряжений ϭx в стойке и ригеле
узла портальной рамы (Polygon)
Однако, в соответствии с данными комплекса Polygon при заданной величине нагрузки область максимальных напряжений |ϭx max|= 0,4506 МПа располагается не в угловой зоне, а в верхней части стойки там, где расположен армирующий каркас с самым мелким шагом 0,0625 м.
Для экспертной оценки результатов численного моделирования обратимся к данным натурного эксперимента [11]. На рис. 17 показан фрагмент узла железобетонной портальной рамы, с аналогичными размерами, в момент разрушения на экспериментальном стенде.
На рис. 18 приведена визуализация моделирования процесса разрушения узла, полученная с помощью комплекса ABAQUS [11].
На приведенной фотографии видны места сколов и сеть магистральных трещин в зоне сопряжения стойки и ригеля. Как отмечается в [11] диагональные трещины возникают первыми и развиваются дальше после появления первого скола на ригеле. Таким образом «очаговый» характер сдвиговых напряжений ϭxz в стойке (рис. 16) согласуется с наблюдаемым на практике сценарием разрушения данного узла.

Рис. 17. Фотография разрушения
портального узла (эксперимент [11])
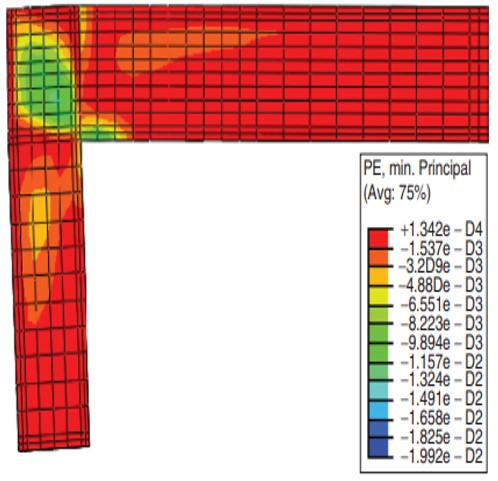
Рис. 18. Прогнозируемый характер
трещин в узле (ABAQUS) [11]
Графики экспериментальных и расчетных зависимостей F∽ux, полученных в [10, 11], показаны на рис. 19.
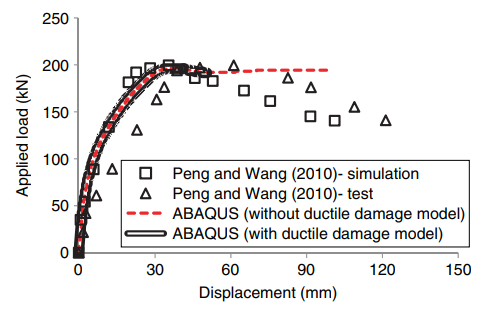
Рис. 19. Графики зависимостей F∽ux [11, 12]
Из рис. 19 следует, разрушение узла происходит при F=200 кН. Соответствующее смещение ригеля составляет порядка 60 мм.
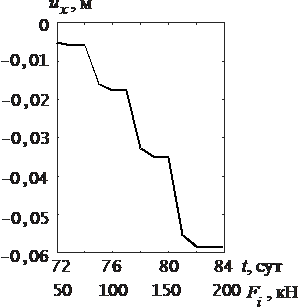
Выполним моделирование рассматриваемого узла портальной рамы с учетом ползучести бетона в рамках модели упруго-ползучего тела. В первом варианте нагружение организуем по четырехступенчатой схеме
Fi=kiF,
где коэффициент принимает значения 0,25; 0,5; 0,75; 1; F=200 кН. Во втором варианте нагрузку прикладываем одномоментно. Полученный график ux∽t приведен на рис. 20 и 21. Сравнивая графики на рис. 20 и 21, устанавливаем, что значения перемещений для каждой ступени нагружения достаточно хорошо согласуются. Таким образом моделирование узла портальной рамы с учетом ползучести позволяет учесть эффекты, связанные с нелинейной деформируемостью бетона. При этом временную координату можно рассматривать как критерий сходимости численного решения. Процесс интегрирования по параметру t можно считать завершенным на i-ом шаге нагружения после выхода кривой ползучести ux∽t на «горизонтальный участок». Экстремальные значения касательных напряжений ϭxz max при нагружении по первому варианту при F=200 кН составили: в стойке -5,244 МПа; в ригеле -2,301 МПа.
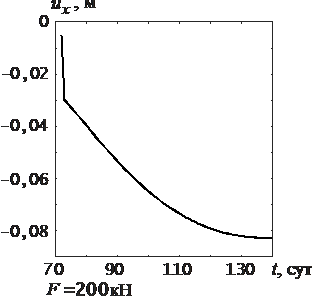
Численное решение при нагружении по второму варианту стабилизируется при t > 130 сут.
|
Рис. 20. График ux∽t |
Рис. 21. График ux∽t |
Здесь следует отметить важный момент относительно оценки несущей способности рассматриваемого узла. Как было отмечено выше, разрушение узла происходит в результате сдвиговых деформаций. Однако современные методики прочностного расчета железобетонных конструкций базируются на двух константах бетона Rb, Rbt – это прочность образца при сжатии и растяжении, т. е. данные о прочности бетона при сдвиге не используются. Обычно полагают, что прочность бетона на срез в 1,5–2 раза больше, чем его прочность на растяжение. Отсюда ϭxz max= 5,244 МПа в 1,3 раза превышает условный предел прочности бетона на срез Rsh=1,5·2,65=3,975 МПа.
Выводы
Выполнена верификация разработанного математического и программного обеспечения, включающая сравнение результатов численных расчетов с имеющимися в литературе экспериментальными данными. В процессе тестирования было установлено, что численное моделирование напряженно-деформированного состояния железобетонных конструкций с учетом ползучести по предлагаемой методике позволяет опосредованно учесть эффекты, связанные с нелинейной деформируемостью бетона. При этом временную координату предлагается рассматривать как условный критерий сходимости, т. е. интегрирование по времени на текущем шаге активного нагружения можно считать завершенным после выхода кривой ползучести на «горизонтальный участок».
1. Alexandrovsky S.V. Calculation of concrete and reinforced concrete structures for tem-perature and humidity changes taking into account creep. M.: Stroyizdat, 1973. 432 p.
2. Gaydzhurov P.P., Iskhakova E.R., Savelyeva N.A. Numerical Simulation of Volumetric Stress-Strain State Prestressed Reinforced Concrete Structures Taking Into Account the Creep of Concrete. // Univ. News. North-Caucas. Reg. Technical Sciences Series. 2023, I. 2. Pp. 17-24 . (In Russ.). DOI: http://dx.doi.org/https://doi.org/10.17213/1560-3644-2023-2-17-24 EDN: https://elibrary.ru/DANZZT
3. Gaijurov P.P., Iskhakova E.R. Certificate of state registration of the computer program No. 201462079. The final definition of the simple goal of the theory of public administra-tion of concrete, taking into account the principle of the President of the Russian Federa-tion-the state and the rapidly accumulating results of the study (Polygon), application No. 2014619750 dated September 26, 2014, Registered November 21, 2014.
4. Design and Stiffness Adaptation Analysis of a Reinforced Concrete Slab // DIANA FEA. URL: https://dianafea.com/tutorial/design-and-stiffness-adaptation-analysis-of-a-reinforced-concrete-slab/
5. David V. Hutton. Fundamentals of Finite Element Analysis. The McGraw Hill Companies, 2004. 494 p.
6. Logan Daryl L. A First Course in the Finite Element Method. University of Wisconsin–Platteville, 2011. 836 p.
7. Ray S.S. Reinforced Concrete. Analysis and Design. Blackwell Science Ltd, 1995. 545 p.
8. DIANA B.V. DIANA 10.7 MANUAL. Delft, Netherlands, Tutorial DIANA FEA. 2023.
9. Crisfield. Variable step-length for nonlinear structural analysis, 1982.
10. Polak. and Vecchio, Nonlinear analysis of reinforced–concrete shells. 1993.
11. Xu Long and Chi King Lee. Modelling of Two Dimensional Reinforced Concrete Beam-Column Joints Subjected to Monotonic Loading. Advances in Structural Engineering, 18(9): 1466–1467, 2015.
12. Clough R. W. «The Finite Element Method in Plane Stress Analysis» // Proc. 2nd ASCE Conf. On Electronic Computation. Pittsburg, Pa. Sept. 1960.