Russian Federation
Russian Federation
This paper presents new formulas for calculating the aerodynamic drag coefficient of lattice structures, which depend on factors such as surface roughness, Reynolds number, and the geometry of the structure. A nonlinear regression method based on logarithmic transformation of the raw data is proposed for determining the shading coefficient. Comparison of the computed results with the normative values given in SP 20.13330.2016 demonstrated that the proposed formulas can be effectively used to calculate the shading coefficient for spatial trusses with tubular profiles at Reynolds numbers below 4·105, without the need to refer to the charts provided in Appendix B of the standard.
aerodynamic drag coefficient, lattice structures, shading coefficient, nonlinear regression, logarithmic transformation, Reynolds number
Введение
Аэродинамические характеристики строительных конструкций являются важным аспектом их надежности и устойчивости, особенно для объектов, подверженных воздействию ветровых нагрузок. Ветровая нагрузка определяется множеством факторов, включая число Рейнольдса, шероховатость поверхности и геометрические параметры конструкции. Расчет и оптимизация аэродинамических коэффициентов, таких как коэффициент лобового сопротивления и коэффициент затемнения, позволяют существенно повысить точность проектирования, а также сократить материальные и трудозатраты [1,6,18].
Решетчатые конструкции, такие как башни и мачты, характеризуются сложным взаимодействием потоков воздуха с элементами конструкции, что требует при проектировании применения экспериментальных, численных и аналитических методов. Исследования аэродинамических характеристик таких объектов включают эксперименты в аэродинамических трубах [13,14], численное моделирование с использованием современных методов, таких как «Computational fluid dynamics» (CFD) [7,16], а также применение нормативных документов, включая СП 20.13330.2016 и EN 1991-1-4:2005 [18,20].
В последние годы акцент сделан на оптимизацию конструктивных решений за счет интеграции данных экспериментальных и численных исследований. Например, исследования ветровых воздействий на башенные сооружения показывают необходимость учета локальных изменений скорости ветра в застройке и их влияния на коэффициенты лобового сопротивления [8,14]. Дополнительно, применение решетчатых конструкций для энергосетевых объектов и телекоммуникационных башен требует разработки новых подходов к расчету устойчивости при экстремальных ветровых условиях, таких как ураганы [16,17].
Методики, основанные на численных и экспериментальных данных, успешно применяются для проектирования уникальных конструкций. Так, использование CFD позволяет учитывать турбулентные явления, которые невозможно отразить при стандартных аналитических расчетах [7,13]. Диссертационные исследования, посвященные анализу аэродинамики башенных сооружений, также демонстрируют перспективность подходов, основанных на адаптивных численных моделях [9,10].
Таким образом, развитие технологий моделирования и стандартизации расчетных методов играет ключевую роль в обеспечении надежности и экономичности современных строительных объектов, подверженных ветровым нагрузкам. Дальнейшие исследования в данной области направлены на интеграцию теоретических и прикладных решений для повышения точности и эффективности расчетов [1,4,19].
Объекты и методы исследования
Объектами исследования в данной работе являются решетчатые конструкции, такие как мачты, башни и опоры ЛЭП, с учетом их аэродинамических характеристик. Основное внимание уделено аэродинамическому коэффициенту лобового сопротивления, который зависит от шероховатости поверхности, числа Рейнольдса и геометрических характеристик конструкции. В качестве конкретных объектов рассмотрены пространственные фермы из трубчатых профилей при числе Рейнольдса менее 4·105.
Исследование включает теоретический анализ, заключающийся в разработке формул для определения аэродинамического коэффициента с учетом различных параметров. Для вычисления коэффициентов затемнения предлогается использовать метод логарифмического преобразования исходных данных и применения нелинейной регрессии. Проведен сравнительный анализ рассчитанных значений коэффициентов затемнения с данными, указанными в СП 20.13330.2016, а также оценена точность предложенных формул по сравнению с графиком В.17 этого нормативного документа. Эмпирические расчеты выполнены для различных типов пространственных ферм, а их результаты использованы для подтверждения разработанных формул. Дополнительно применены методы регрессионного анализа для построения зависимостей аэродинамического сопротивления от ключевых параметров конструкции.
Результаты исследований
Согласно [1,3] аэродинамический коэффициент лобового сопротивления
Здесь
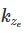 — коэффициент, учитывающий изменение ветрового давления для высоты
— коэффициент, учитывающий изменение ветрового давления для высоты
Примем максимальную высоту
Выразив диаметр трубы d через приведенные параметры, получим в метрах:
Следовательно, для конструкций с диаметром элементов не более 0.73 м и высотой до 100 м, аэродинамический коэффициент лобового сопротивления
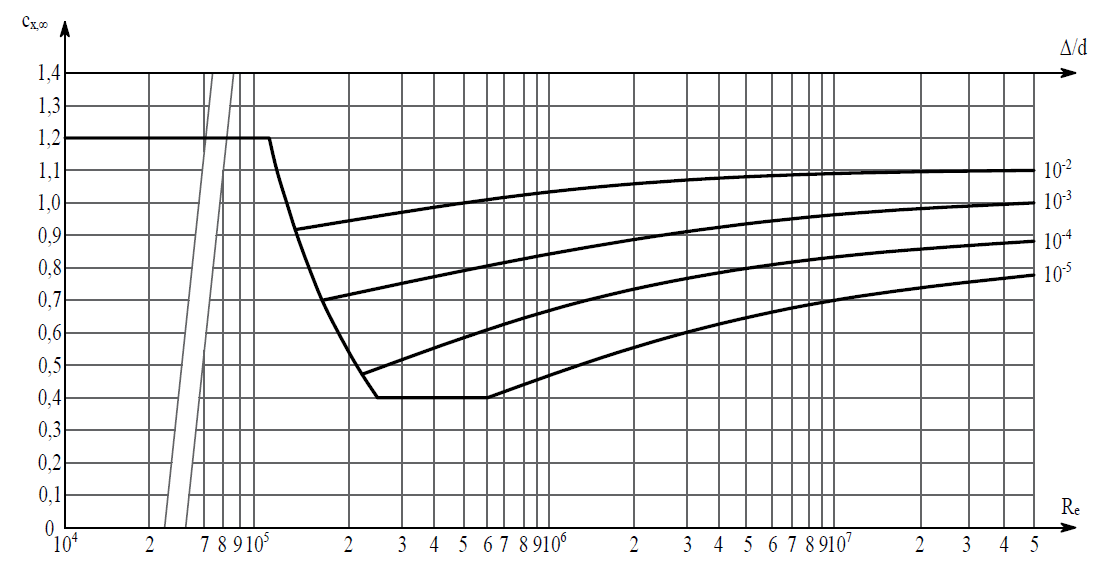
Рис. 1. Определение
Аэродинамические коэффициенты
Аэродинамические коэффициенты
коэффициент заполнения ферм
$$\varphi=\frac{\sum A_i}{A_k}.$$
Коэффициент затемнения
Таблица 1
Коэффициент затемнения
|
|
|
||||
|
1/2 |
1 |
2 |
4 |
6 |
|
|
0,1 |
0,93 |
0,99 |
1 |
1 |
1 |
|
0,2 |
0,75 |
0,81 |
0,87 |
0,9 |
0,93 |
|
0,3 |
0,56 |
0,65 |
0,73 |
0,78 |
0,83 |
|
0,4 |
0,38 |
0,48 |
0,59 |
0,65 |
0,72 |
|
0,5 |
0,19 |
0,32 |
0,44 |
0,52 |
0,61 |
|
|
0 |
0,15 |
0,3 |
0,4 |
0,5 |
Принятые в таблице обозначения проиллюстрированы на Рис. 2.
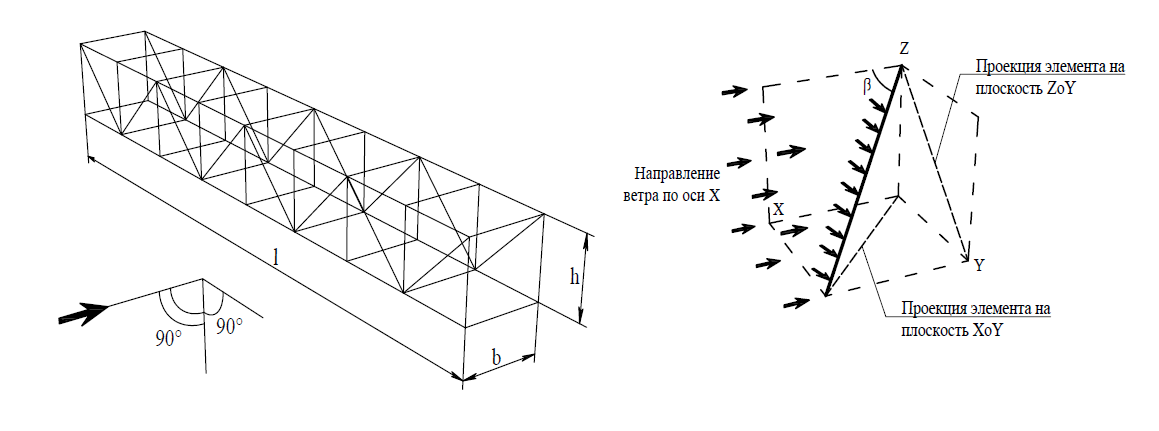
Рис. 2. Габаритные размеры решетчатой конструкции
Для значений
Предложена следующая формула
где
При
Коэффициенты
Таблица 2
Коэффициент затемнения
|
|
|
||||
|
1/2 |
1 |
2 |
4 |
6 |
|
|
0,1 |
0,91 |
0,94 |
0,95 |
0,96 |
0,97 |
|
0,2 |
0,81 |
0,83 |
0,86 |
0,89 |
0,92 |
|
0,3 |
0,56 |
0,70 |
0,74 |
0,81 |
0,86 |
|
0,4 |
0,34 |
0,53 |
0,60 |
0,70 |
0,78 |
|
0,5 |
0,20 |
0,35 |
0,44 |
0,58 |
0,69 |
|
|
0,11 |
0,14 |
0,26 |
0,45 |
0,59 |
Результаты сравнения нормативных значений
Таблица 3
Коэффициент затемнения η
|
|
|
||||
|
1/2 |
1 |
2 |
4 |
6 |
|
|
0,1 |
-2% |
-5% |
-5% |
-4% |
-3% |
|
0,2 |
6% |
2% |
-1% |
-1% |
-1% |
|
0,3 |
0% |
5% |
1% |
3% |
3% |
|
0,4 |
-4% |
5% |
1% |
5% |
6% |
|
0,5 |
1% |
3% |
0% |
6% |
8% |
|
|
10% |
-1% |
-4% |
5% |
9% |
Сравнение результатов продемонстрировало, что предложенные формулы могут быть использованы для вычисления коэффициента затемнения
Выводы
В результате проведенного исследования было предложено новое решение для определения аэродинамического коэффициента лобового сопротивления решетчатых конструкций, учитывающее такие параметры, как шероховатость поверхности, число Рейнольдса и геометрические характеристики объекта. Предложенные формулы позволяют эффективно вычислять коэффициент затемнения для пространственных ферм из трубчатых профилей при числе Рейнольдса менее 4·105 без необходимости использования графика В.17 СП 20.13330.2016. Метод нелинейной регрессии, основанный на логарифмическом преобразовании данных, продемонстрировал свою высокую точность и применимость в расчете аэродинамических коэффициентов. Сравнение полученных значений с коэффициентами, приведенными в нормативном документе, подтвердило адекватность предложенной методики. Это позволяет эффективно рассчитывать аэродинамическое сопротивление решетчатых конструкций, что имеет большое значение для повышения их устойчивости и надежности в различных инженерных приложениях.
1. Ioskevich A.V., Savchenko A.V., Egorova E.S., Ioskevich V.V. Wind pressure reduction factor and its consideration in the design of lattice structures // Construction of Unique Buildings and Structures. 2015. No. 4(31). P. 45–57. DOI: https://doi.org/10.18720/CUBS.31.3. EDN: https://elibrary.ru/UISIAF
2. Gagarin V.G., Guvernyuk S.V., Ledenyev P.V. Aerodynamic characteristics of buildings for calculating wind effects on enclosing structures // Housing Construction. 2010. No. 1. URL: https://cyberleninka.ru/article/n/aerodinamicheskie-harakteristiki-zdaniy-dlya-rascheta-vetrovogo-vozdeystviya-na-ograzhdayuschie-konstruktsii (accessed: 08.12.2024). EDN: https://elibrary.ru/MSUTYB
3. Poddaeva O.I., Buslaeva Y.S., Gribach D.S. Experimental study of wind loads on a multifunctional high-rise residential complex // Bulletin of BSTU named after V.G. Shukhov. 2014. No. 6. URL: https://cyberleninka.ru/article/n/eksperimentalnoe-issledovanie-vetrovyh-nagruzok-na-mnogofunktsionalnyy-vysotnyy-zhiloy-kompleks (accessed: 08.12.2024). EDN: https://elibrary.ru/TCRYQL
4. Poddaeva O.I., Dunichkin I.V. Architectural and structural aerodynamics // Bulletin of MGSU. 2017. No. 6(105). URL: https://cyberleninka.ru/article/n/arhitekturno-stroitelnaya-aerodinamika (accessed: 08.12.2024).
5. Andre C., Costa F., Paiva R., Barros R. Aerodynamic Study of Wind Flow through a Lattice Tower of Angular Section Profiles, Using Computational Fluid Dynamics // Proceedings of the 2014 International Conference on Mechanics and Civil Engineering. 2014. P. 83–87. DOI: https://doi.org/10.2991/ICMCE-14.2014.15.
6. Sui Q., Sun Q., Yang J., Wang S. Analysis and Optimization of Wind Resistance Parameters for Lattice-Type High-Modulus Supports Based on the Optimal Criteria Method // Stavební obzor - Civil Engineering Journal. 2023. Vol. 32. P. 533–548. DOI: https://doi.org/10.14311/CEJ.2023.04.0040. EDN: https://elibrary.ru/BXRUQP
7. Pashkov D.E., Varibrus D.S. Calculation of wind effects using CFD modeling // Innovative Science. 2019. No. 12. URL: https://cyberleninka.ru/article/n/vychislenie-vetrovyh-vozdeystviy-putyom-primeneniya-cfd-modelirovaniya (accessed: 08.12.2024). EDN: https://elibrary.ru/JABDBU
8. Olyenkov V.D., Tazeev N.T. Wind load calculation considering local wind speed changes in urban development // Bulletin of South Ural State University. Series: Construction and Architecture. 2019. No. 4. URL: https://cyberleninka.ru/article/n/raschet-vetrovyh-nagruzok-s-uchetom-lokalnyh-izmeneniy-skorosti-vetra-v-zastroyke (accessed: 08.12.2024). DOI: https://doi.org/10.14529/build190401; EDN: https://elibrary.ru/CDLLXE
9. Badertdinov I.R. Triangular lattice structures: Ph.D. dissertation. Rostov-on-Don, 2020. 21 p. EDN: https://elibrary.ru/CWYSQC
10. Sabitov L.S. Tower structure design: DSc. dissertation. Rostov-on-Don, 2021. 38 p. EDN: https://elibrary.ru/SEUZJW
11. Szafran J., Juszczyk K., Kamiński M. Reinforcements of Tower Structures: Effective and Economic Design Engineering // Lightweight Structures in Civil Engineering. Contemporary Problems. Proceedings of XXIV LSCE 2018. Lodz: Łódź University of Technology, 2018. P. 126–133.
12. Diaconita A.I., Rusu L., Andrei G. A Local Perspective on Wind Energy Potential in Six Reference Sites on the Western Coast of the Black Sea Considering Five Different Types of Wind Turbines // Inventions. 2021. Vol. 6, no. 3. P. 44. DOI:https://doi.org/10.3390/inventions6030044. EDN: https://elibrary.ru/VKZIIF
13. Wind Load Investigation of Self-Supported Lattice Transmission Tower Based on Wind Tunnel Tests / W. Zhang [et al.] // Engineering Structures. 2022. Vol. 252. P. 113575. DOI: https://doi.org/10.1016/j.engstruct.2021.113575. EDN: https://elibrary.ru/LJNXDT
14. Research on Wind Load Characteristics on the Surface of a Towering Precast Television Tower with a Grid Structure Based on Large Eddy Simulation / P. Wu [et al.] // Buildings. 2022. Vol. 12, no. 9. P. 428. DOI: https://doi.org/10.3390/buildings12091428. EDN: https://elibrary.ru/FJSQVE
15. Failure Criteria and Wind-Induced Vibration Analysis for an Offshore Platform Jacking System / H.-N. Li [et al.] // International Journal of Structural Stability and Dynamics. 2021. P. 2150105. DOI: https://doi.org/10.1142/S0219455421501054. EDN: https://elibrary.ru/GQYSUL
16. A Method for Analyzing Stability of Tower-Line System under Strong Winds / B. He [et al.] // Advances in Engineering Software. 2019. Vol. 127. P. 1–7. DOI: https://doi.org/10.1016/j.advengsoft.2018.10.004.
17. Dynamic Analysis of Self-Supported Tower under Hurricane Wind Conditions / I. Fernández Lorenzo [et al.] // Journal of Wind Engineering and Industrial Aerodynamics. 2020. Vol. 197. P. 104078. DOI: https://doi.org/10.1016/j.jweia.2019.104078. EDN: https://elibrary.ru/MEZHDB
18. SP 20.13330.2016 “SNiP 2.01.07-85* Loads and Impacts”. Moscow: Ministry of Construction of Russia, 2016. 79 p.
19. Berezin M.A., Katyushin V.V. Atlas of Aerodynamic Characteristics of Building Structures. N.: LLC “Olden-Polygraphy”, 2002. 129 p.
20. EN 1991-1-4:2005. Eurocode 1: Actions on Structures – Part 1-4: General Actions – Wind Actions. Brussels: CEN, 2005. 123 p.



















