г. Санкт-Петербург и Ленинградская область, Россия
г. Москва и Московская область, Россия
Россия
г. Санкт-Петербург и Ленинградская область, Россия
УДК 691.327-478 Пустотелые бетонные изделия
ГРНТИ 67.01 Общие вопросы строительства
Цель исследования – разработка и верификация математической модели цементно-песчаной матрицы бетона с ауксетической возвратно-вогнутой структурой для повышения энергопоглощающих свойств строительных материалов, применяемых в специальных сооружениях Гражданской обороны Российской Федерации. Работа основана на анализе физико-механических характеристик композитных материалов, модифицированных пустотами различной геометрии, с учетом требований к защитным конструкциям, работающим при повышенных динамических нагрузках техногенного характера. Методы включают математическое моделирование методом конечных элементов для создания верифицированной модели цементно-песчаной матрицы бетона класса по прочности на сжатие В30 и В60. Верификация проводилась путем сравнения результатов моделирования с данными реальных испытаний на прессе, с заданием граничных условий, физико-механических свойств материалов и параметров нагружения. Для ауксетической структуры применялись возвратно-вогнутые ячейки с углом вогнутости 60° и длиной ребра 15 мм, моделируемые для кубов различных размеров (масштабирование и наложение ячеек). Результаты демонстрируют равномерное распределение напряжений в ауксетической структуре цементно-песчаной матрицы без эффекта «обоймы», характерного для стандартного бетона, с снижением прочности на сжатие (до 8,7 МПа для В30 и 17,4 МПа для В60) при увеличении деформативности до 10 раз. Диаграммы напряжение-деформация подтверждают повышенную податливость, а соответственно и энергопоглощение. Практическая значимость заключается в применении модели для проектирования энергопоглощающих защитных конструкций специальных сооружений, повышающих их защищенность.
метаматериалы, ауксетические структуры, цементно-песчаная матрица, математическое моделирование, энергопоглощение, метод конечных элементов, бетонные конструкции, динамические нагрузки, защитные сооружения.
Введение
Метаматериалы с искусственно созданными структурами открывают новые возможности для управления энергией в строительных материалах и конструкциях. Особый интерес представляют ауксетики – материалы с отрицательным коэффициентом Пуассона, которые при сжатии уплотняются в поперечном направлении, повышая локальную плотность и поглощая энергию удара. Это свойство обеспечивает повышенную ударопрочность, устойчивость к разрушению и энергопоглощение, делая ауксетические структуры перспективными для применения в строительстве, включая специальные сооружения.
В контексте специальных сооружений, энергопоглощающие материалы необходимы для повышения податливости конструкций под динамическими нагрузками от техногенных катастроф и аварий на больших производствах. Традиционные бетоны по СП63.13330.2018 обладают ограниченными свойствами, поэтому модификация цементно-песчаной матрицы ауксетическими пустотами (ре-энтрант типа) позволяет оптимизировать поведение под нагрузкой [2].
Настоящая работа фокусируется на математическом моделировании для верификации и анализа таких структур.
Математическое моделирование
Разработка верифицированной математической модели ЦПМ бетона проводилась в программном комплексе ANSYS Static Structural, что позволило учесть нелинейные эффекты деформации и распределения напряжений в композитном материале. Алгоритм моделирования представлен на Рис. 1.
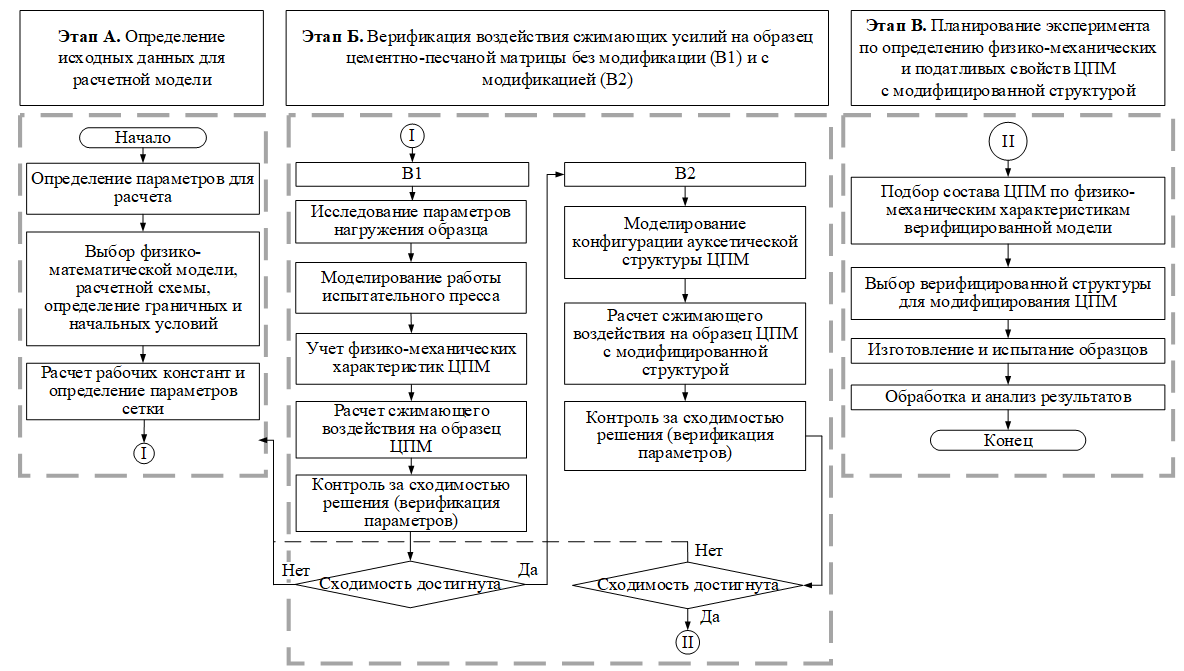
Рис. 1. Алгоритм планирования эксперимента по определению физико-механических характеристик модифицированных материалов
Модель цементно-песчаной матрицы создавалась для бетонов классов В30 и В60 в соответствии с требованиями ГОСТ 10180 и СП63.13330.2018 (Табл. 1), где указаны модуль упругости, коэффициент Пуассона, предел прочности на сжатие и другие характеристики.
Таблица 1
Характеристики цементно-песчаной матрицы бетона
|
Материал |
Плотность, |
Коэффициент |
Модуль упругости, |
Предел прочности |
Угол дилатансии, |
|---|---|---|---|---|---|
|
Бетон В30 |
2300 |
0,2 |
30 |
30 |
35 |
|
Бетон В60 |
2600 |
0,2 |
39,5 |
60 |
35 |
Для обеспечения точности модели применялась сетка, адаптированная к геометрии образцов (кубы 100×100×100 мм, 200×200×200 мм и 300×300×300 мм) для минимизации ошибок дискретизации и соответствует рекомендациям по моделированию ауксетических структур в ANSYS [1, 2]. Верификация модели осуществлялась путем сравнения результатов численного анализа с данными реальных испытаний на гидравлическом прессе в соответствии с ГОСТ 10180, после чего вносились корректировки в параметры материала для достижения сходимости.
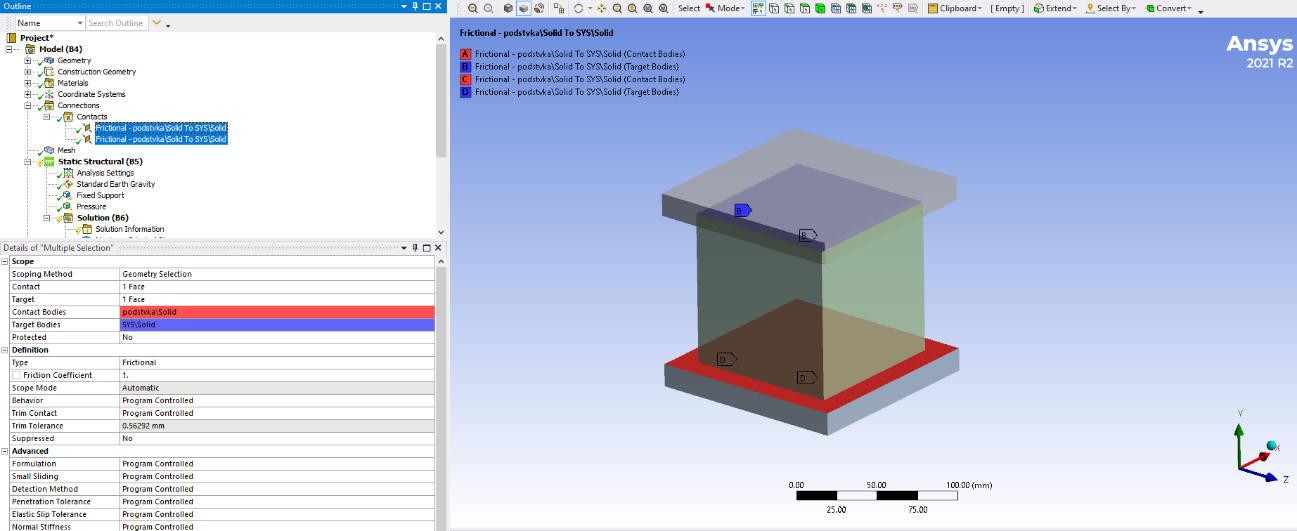
Рис. 2. Моделирование работы испытательного пресса
Граничные условия и нагружение модели задавались в полном соответствии «реальному» эксперименту. Для моделирования испытания на прессе, были смоделированы две металлический пластины из конструкционной стали (Рис. 2).
Для качественной работы конструкции были заданы характеристики стальных пластин (Табл. 2).
Таблица 2
Физико-механические характеристики конструкционной стали пластин моделируемого испытательного пресса
|
Плотность, кг/м² |
Коэффициент Пуассона |
Модуль упругости, |
Предел прочности |
Предел текучести |
|---|---|---|---|---|
|
7850 |
0,3 |
20 |
460 |
250 |
После определения параметров для расчета задаются параметры нагружения образца (Табл. 3).
Таблица 3
Энергетическая характеристика катиона сырья (ОЭО)
|
Наименование |
Заданная характеристика |
|---|---|
|
Сила сжатия модели |
30 МПа; 60 МПа |
|
Устойчивость модели |
функция «Fixed |
|
Расчетная сетка |
размер ячеек сетки 10 мм |
|
Количество подшагов нагружения |
100 |
|
Тип решателя |
«Directive» |
|
Трение |
0,2 |
Моделирование конфигурации ауксетической структуры цементно-песчаной матрицы проводилось по следующим положениям (Рис. 3):
- Первое положение основано на создании оптимальной геометрии ячейки для повышения энергопоглощения и программируемого разрушения. Это возможно в ауксетических структурах с отрицательным коэффициентом Пуассона, которые по геометрии максимально схожи с картиной разрушения бетонных образцов.
- Второе положение заключается в том, что разрабатываемая ауксетическая структура должна сравниваться с сотовыми структурами правильной формы, типа круга или квадрата исходя из экономичности производства подобных конструкций к эффективности их применения в качестве энергопоглощающих.
- Третье положение основано на принципе сохранения площади поперечного сечения сравниваемых типов пустот и количеству материала, участвующего в работе по сопротивлению сжимающим напряжениям.
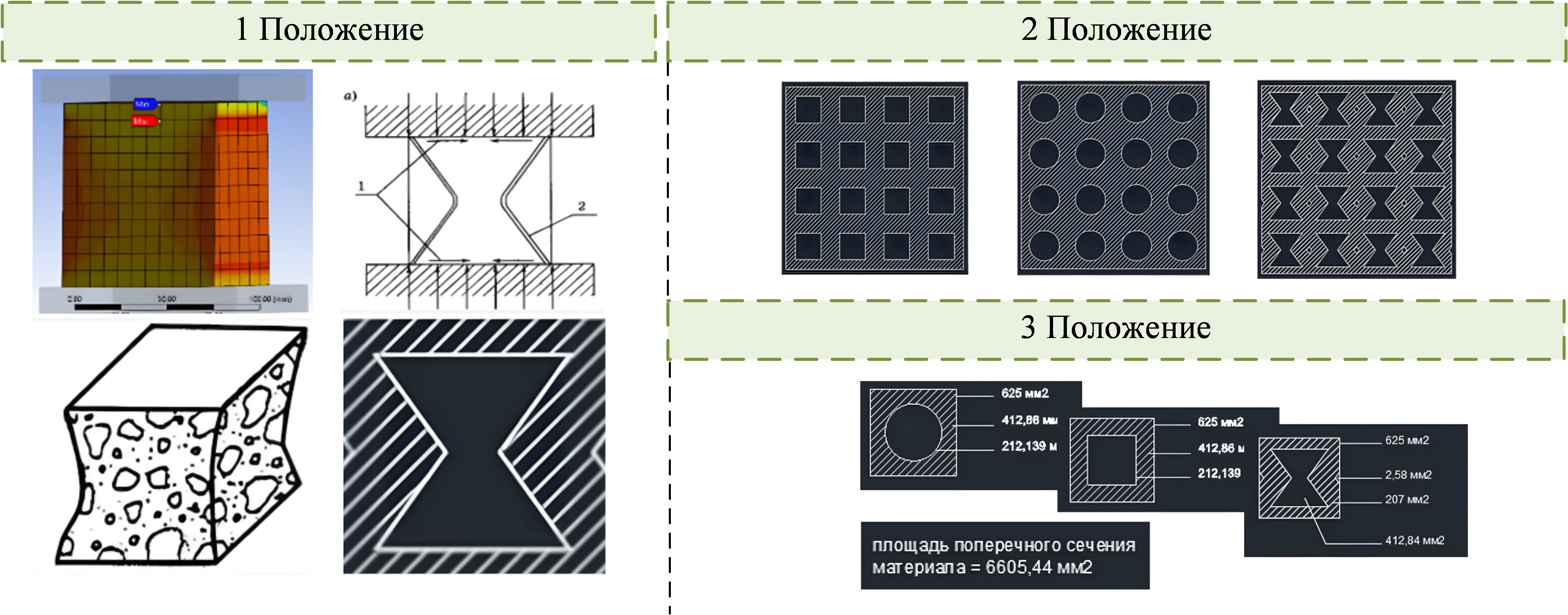
Рис. 3. Моделирование конфигурации ауксетической структуры ЦПМ
Моделирование проводилось с двумя подходами: масштабирование ячеек (увеличение размеров в 2–6 раз) и их наложение «друг на друга» (многослойная конфигурация), что позволяет оценить влияние геометрии на энергопоглощение [3].
Экспериментальные исследования проводились на гидравлическом прессе, в соответствии с ГОСТ 10180 и ГОСТ 26633. Образцы ЦПМ изготавливались из цемента М500, песка (фракция 0,63) и воды (В/Ц=0,45), с модификацией ауксетическими пустотами путем установки съемных цилиндров перед бетонированием.
Результаты
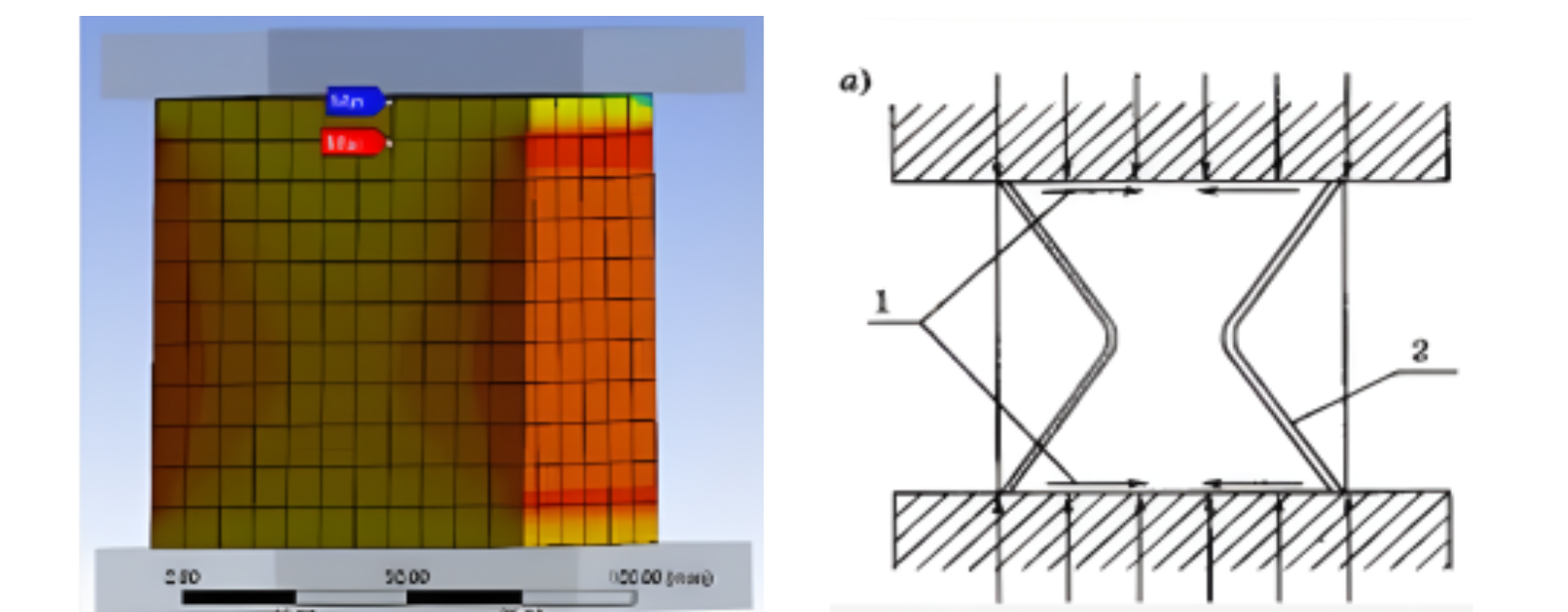
Математическое моделирование стандартной цементно-песчаной матрицы бетона класса В30 и В60 в ANSYS Static Structural показало, что разрушение образцов происходит при напряжениях σ=28,5 МПа для В30 и σ=58,5 МПа для В60, что соответствует требованиям
ГОСТ 10180 и СП63.13330.2018. Распределение внутренних напряжений в модели
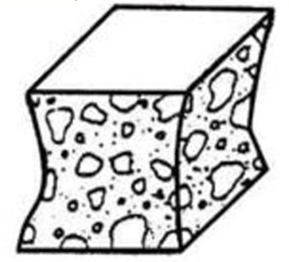
(Рис. 4а) демонстрирует типичный для традиционного бетона эффект «обоймы», где силы трения уменьшаются по мере удаления от торцевых граней, приводя к разрушению в форме четырех усеченных пирамид, сомкнутых малыми основаниями, как описано в
ГОСТ 10180 (Рис. 4б).
 |
 |
|
а) |
б) |
Рис. 4. Распределение внутренних напряжений при испытании на одноосное сжатие:
а) Результат моделирования испытания образца ЦПМ;
б) Характер разрушения ЦПМ по ГОСТ 10180-2012
Диаграмма напряжение-деформация (Рис. 5а) подтверждает приближение к реальным образцам (Рис. 5б), с верификацией модели по критериям прочности и характера разрушения.
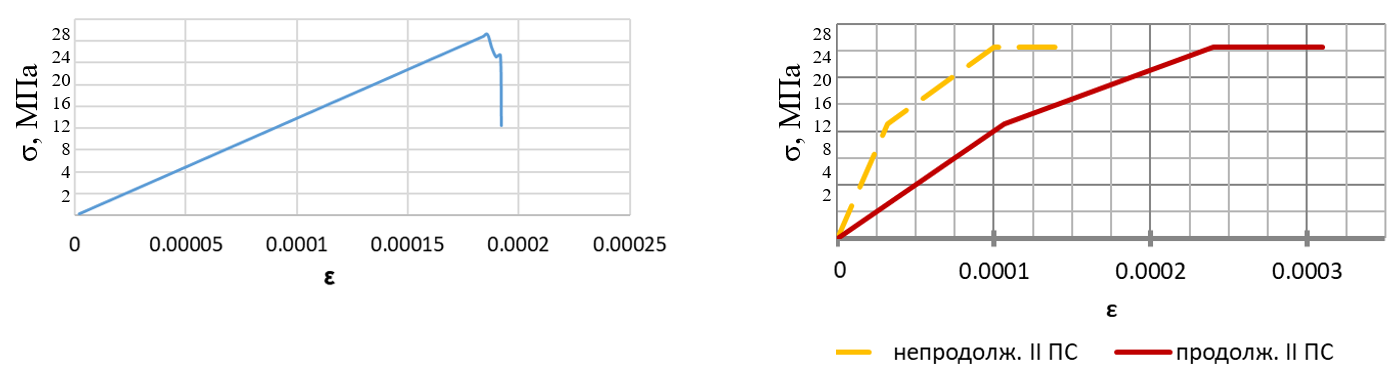
Рис. 5. Диаграммы разрушения образцов:
а) Математическая модель ЦПМ; б) Реальный образец ЦПМ по ГОСТ
Для ауксетической структуры на основе возвратно-вогнутых ячеек, моделируемой в кубах размерами 100×100×100 мм, 200×200×200 мм и 300×300×300 мм (Рис. 6), анализ выявил отсутствие эффекта «обоймы» и более равномерное распределение нагрузки благодаря уникальной геометрии, перенаправляющей напряжения между элементами (Рис. 7а).
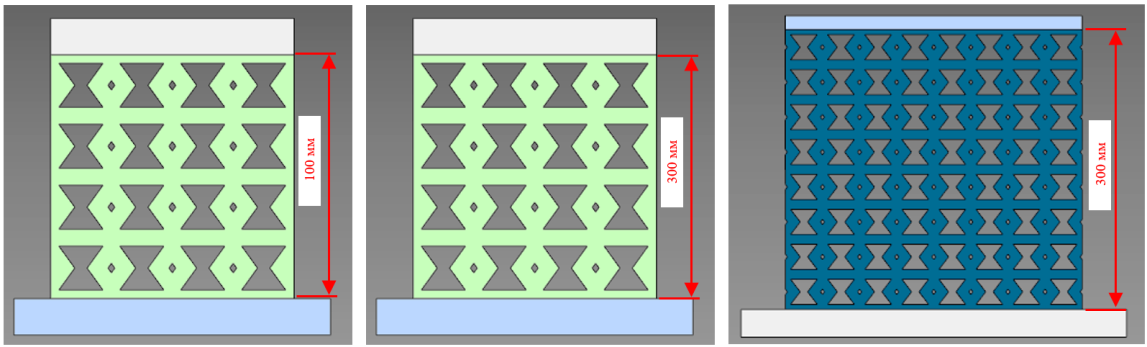
Рис. 6. Распределение внутренних напряжений при испытании на одноосное сжатие:
а) исходная структура; б) структура в масштабе; в) структура «друг на друге»
Это согласуется с исследованиями ауксетических метаматериалов в цементно-основанных композитах, где такая структура снижает концентрацию деформаций в центральной зоне [3, 5-8].

Рис. 7. Результат расчета модели ЦПМ с ауксетической структурой:
а) распределение напряжений в ауксетической структуре;
б) распределение деформаций ауксетической структуре;
в) распределение деформаций в верифицированном образце
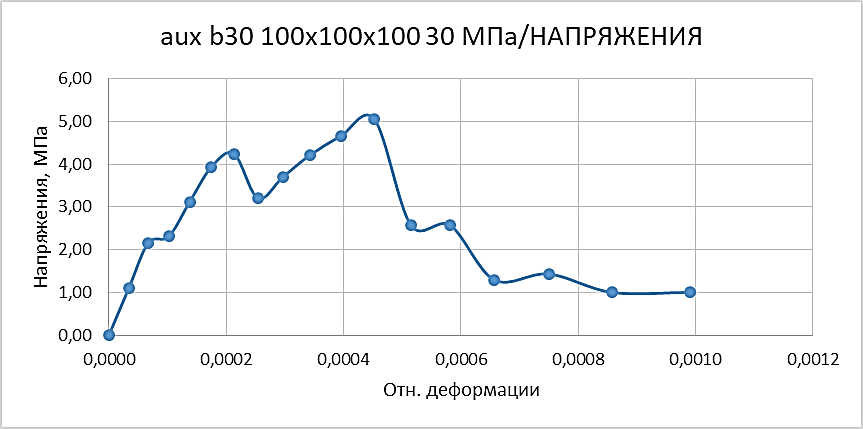
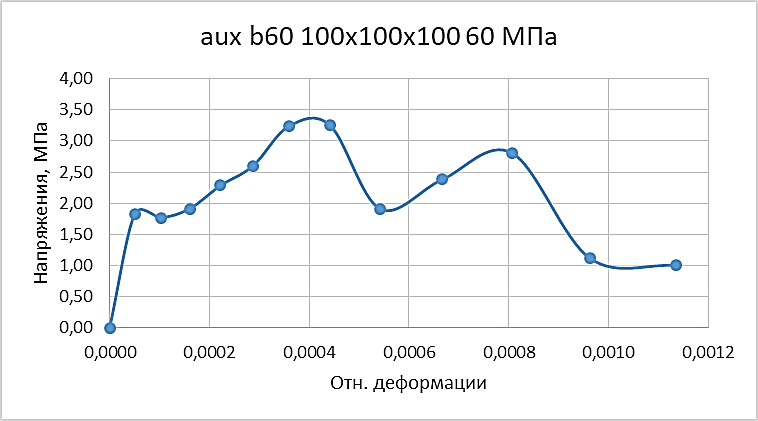
Разрушение модифицированных образцов происходит при напряжениях 8,7 МПа для В30 и 17,4 МПа для В60, что указывает на снижение прочности на сжатие в 3,3 раза для В30 и 3,4 раза для В60 по сравнению со стандартными образцами. Однако деформативность увеличивается до 10 раз, как показано на диаграммах σ-ε (Рис. 8а для В30 и Рис. 8б для В60), где податливость материала возрастает, обеспечивая повышенное энергопоглощение в ~5,6–6,85 раза.
 |
 |
| а) | б) |
Рис. 8. Диаграмма σ-ε цементно-песчаной матрицы,
модифицированной ауксетическими цилиндрами:
а) для бетона В30; б) для бетона В60
Полученные результаты позволяют прогнозировать поведение многопустотных плит покрытия специальных сооружений под динамическими нагрузками от воздействий аварийного техногенного характера.
Обсуждение
Проведенное исследование демонстрирует перспективу применения ауксетических метаматериалов в модификации цементно-песчаных матриц для повышения их энергопоглощающих свойств. Разработанная и верифицированная математическая модель стандартного бетона (В30 и В60) в ANSYS по результатам совпадает с экспериментальными данными по прочности, характеру разрушения и распределению напряжений. Это позволило перейти к моделированию возвратно-вогнутых ауксетических структур, которые, несмотря на снижение прочности (5,05 МПа для В30 и 3,25 МПа для В60), продемонстрировали принципиально иное поведение: равномерное распределение напряжений, отсутствие концентрации деформаций в центре и повышенную устойчивость к динамическим нагрузкам за счет уникальной геометрии ячеек.
1. Lakes R.S. Foam structures with a negative Poisson's ratio // Science. 1987. Vol. 235. P. 1038–1040. DOI: https://doi.org/10.1126/science.235.4792.1038; EDN: https://elibrary.ru/IDWSBR
2. Ren X., Das R., Tran P., Ngo T.D., Xie Y.M. Auxetic metamaterials and structures: A review // Smart Materials and Structures. 2018. Vol. 27, no. 2. Article 023001.
3. Структурное моделирование метаматериалов: монография / В.И. Ерофеев, И.С. Павлов. Нижний Новгород: ИПФ РАН, 2019. 196 с.
4. Zhong R., Ren X., Zhang X.Y., Luo C., Zhang Y., Xie Y.M. Mechanical properties of concrete composites with auxetic single and layered honeycomb structures // Construction and Building Materials. 2022. Vol. 322. P. 126453. DOI: https://doi.org/10.1016/j.conbuildmat.2022.126453; EDN: https://elibrary.ru/YCEKPP
5. Luo C., Ren X., Han D., Zhang X.G., Zhong R., Zhang X.Y., Xie Y.M. A novel concrete-filled auxetic tube composite structure: Design and compressive characteristic study // Engineering Structures. 2022. Vol. 268. P. 114759. DOI: https://doi.org/10.1016/j.engstruct.2022.114759; EDN: https://elibrary.ru/RDMNFP
6. Choudhry N.K., Panda B., Kumar S. In-plane energy absorption characteristics of a modified re-entrant auxetic structure fabricated via 3D printing // Composites Part B: Engineering. 2022. Vol. 228. P. 109437. DOI: https://doi.org/10.1016/j.compositesb.2021.109437; EDN: https://elibrary.ru/KXVPBK
7. Zhang J., Lu G., You Z. Large deformation and energy absorption of additively manufactured auxetic materials and structures: A review // Composites Part B: Engineering. 2020. Article 108340. DOI: https://doi.org/10.1016/j.compositesb.2020.108340
8. Gao Y., Wei X., Han X., Zhou Z., Xiong J. Novel 3D auxetic lattice structures developed based on the rotating rigid mechanism // International Journal of Solids and Structures. 2021. Vol. 233. Article 111232. DOI: https://doi.org/10.1016/j.ijsolstr.2021.111232; EDN: https://elibrary.ru/VWXIDU



















