Екатеринбург, Свердловская область, Россия
Екатеринбург, Свердловская область, Россия
ББК 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
В статье обсуждаются особенности определения параметров жесткости нескальных грунтов, которые в отличие от скальных грунтов имеют сложный, физически нелинейный характер деформирования. Значения параметров жесткости этих грунтов следует определять по результатам полевых (in-situ) испытаний. Метод определения параметров нелинейной модели, позволяющий получать единственный, физически корректный результат и учитывающий также фактор геометрической нелинейности был использован для решения практических проблем, решение которых в рамках теории линейного деформирования невозможно
грунт, нелинейность, параметры, метод, практическое применение
Расчеты грунтовых оснований, а значит и проектирование оснований и фундаментов сооружений должны выполняться с учетом особенностей грунтовой среды. Сейчас на это прямо указывает требование статьи 16 Федерального закона №384-ФЗ «Регламента о безопасности зданий и сооружений», а с 1974 года, начиная со Строительных норм и правил СНиП II-15-74, затем в СНиП 2.02.01-83*, а сейчас в СП 22.13330.2011 это положение в виде рекомендации присутствует в общих указаниях по проектированию оснований и фундаментов. Главная особенность грунтов состоит в их природном происхождении. Результатом разнообразного генезиса, прежде всего нескальных грунтов, являются, кардинально отличающие их от, так называемых, конструкционных материалов (металлов, бетонов, резины и т.п.) следующие особенности: во-первых уникальность, в какой-то степени сравнимая с биологической эндемичностью (особенно по механическим свойствам – результатом многосложного генезиса); во-вторых, ярко выраженный сложный, так называемый, физически нелинейный характер деформирования, именно ввиду значительно более слабых внутренних связей по сравнению с конструкционными материалами (у песка, например, эти связи практически полностью отсутствуют). Из-за этого же физическая нелинейность грунтов в значительно большей степени, чем у конструкционных материалов, определяется изменением прочности. Феноменологическое различие в деформировании конструкционных материалов и грунтов иллюстрируется диаграммами рисунков 1 и 2.
Рис.1. Линейное деформирование конструкционных материалов (K = const, G = const)
Рис.2. Нелинейное деформирование грунта (KKconst, GKconst)
На диаграммах рисунков 1, 2 и 3 использованы следующие обозначения: , ; 
– первые инварианты тензоров напряжений и деформаций, соответственно (объемная деформация); i, i – вторые инварианты девиаторных частей тензоров напряжений и деформаций, соответственно (деформация формоизменения-сдвига); K= – модуль объемной деформации; G = – модуль сдвига.
Исторически сложилось так, что из-за близкого к линейному виду графиков осадки грунта S от действующего на него давления P, особенно у плотных грунтов, для расчета деформаций нескальных грунтов была принята удобная в условиях отсутствия ЭВМ теория линейного деформирования Гука-Юнга, тем более, что ранее для расчета деформаций грунтов уже применялись также линейная теория Фусса-Винклера, а для расчета их прочности линейная теория Кулона. Графическая интерпретация линейных зависимостей для грунта приведена на рисунке 3.
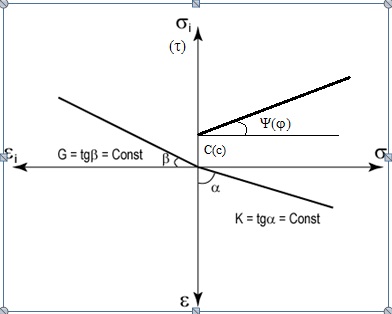
- Графическая интерпретация системы линейных деформационной и прочностных моделей грунта (деформационная модель Гука-Юнга изображена в четвертях s - e и si - ei, а прочностная модель – в четверти s - si: в скобках даны обозначения для версии закона прочности Кулона, вне скобок – для версии закона прочности Мизеса)
- позже, когда стало возможным выполнять сложные расчеты грунтовых оснований на ЭВМ [1,2,3,4], стало ясно, что график зависимости осадки грунта S от давления P (интегральная кривая) может иметь близкий к линейному вид и при сложных нелинейных соотношениях между относительными деформациями eij и напряжениями sij (определяющие дифференциальные соотношения), иллюстрируемые графиками на рисунке 2. Физическая же нелинейность грунта проявляется главным образом: в сложности распределения контактных напряжений под подошвой фундаментов и в массиве грунта из-за зависимости этих распределений от жесткости грунта в различных точках массива, определяемой соотношениями что определяет, например, величину и форму сжимаемой зоны под фундаментами, а значит и влияние ее на соседние сооружения и подземные коммуникации. Вместе с тем, упомянутое выше требование статьи 16 Федерального закона №384-ФЗ и рекомендации Строительных норм и правил о необходимости учета при проектировании физической, геометрической (большие деформации) нелинейностей, а также реологических особенностей деформирования грунтов противоречат другим положениям Строительных норм и правил, в которых для расчета деформаций грунтов предлагаются расчетные способы на базе теории линейного деформирования грунта (Гука-Юнга), т.е. той же теории, что и для расчета деформаций резины, металла, бетона и других подобных им материалов. Понятно, что это создает серьезные проблемы при проектировании фундаментов и других геотехнических сооружений, прежде всего, проблемы, связанные с адекватностью расчетов, а значит c обоснованностью и надежностью основанных на них проектных решений; а ведь геотехническая часть сооружения (в частности основание) является неотъемлемым и при этом несущим, часто самым деформируемым его элементом. Естественно, что возникают при этом и проблемы при прохождении строительных экспертиз, в том числе экспертизы результатов инженерно-геологических изысканий. Одна из таких проблем связана с определением величины модуля Юнга (модуля деформации) грунта. Согласно фундаментальным положениям механики сплошной среды деформация любой, в том числе грунтовой среды (а механика грунтов – это один из разделов механики сплошной среды) характеризуется минимум двумя жесткостными характеристиками. При этом гипотеза линейной деформации предполагает наличие двух независимых от напряженно-деформированного состояния (НДС) среды констант. Такими константами могут быть либо модуль линейной деформации Гука-Юнга E и коэффициент Пуассона n либо, упоминавшиеся выше модуль объемной деформации K и модуль сдвига G. Поскольку и та и другая пары констант характеризуют один и тот же феномен деформации среды, то эти величины могут быть взаимооднозначно выражены друг через друга, например, величины E и v можно определить через величины K и G [5]:
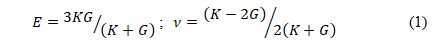
Конечно физический смысл величин K (деформация объема) и G (деформация формы-сдвиг) более очевиден, чем физический смысл величин и G, отражающих, как следует из формул (1), комбинацию указанных двух составляющих деформации. При этом в разных схемах испытания грунтов, для разных видов грунта и даже на разных глубинах в одном и том же грунте эти деформации присутствуют в разных пропорциях, что собственно и объясняет различие значений модуля деформации E в разных типах испытаний и на разных глубинах [6,7]. Это различие становится еще более понятным, если обратиться к зависимостям величин K и G от напряженного состояния, что имеет свое математическое выражение и объяснение в рамках моделей нелинейного деформирования грунта, например, модели Боткина [8,9,2,4,10], включенной в Межгосударственный стандарт ГОСТ 12248-2010:
Здесь – закон прочности грунта в форме Мизеса – Боткина
- – константы нелинейной модели грунта) и, как указывалось выше,
; 
– первые инварианты тензоров напряжений и деформаций, соответственно; ; – вторые инварианты девиаторных (формоизменение) частей тензоров напряжений и деформаций, соответственно). Таким образом, согласно формулам (1 и 2) на самом деле в различных типах испытаний определяются разные деформационные параметры, носящие одно и то же общее название – «модуль деформации» (поэтому в научно-технической литературе часто применяют уточняющие, а по сути верные названия: «полевой модуль деформации», «штамповые модули деформации для штампов разных размеров», «прессиометрический модуль деформации, «компрессионный модуль деформации», «стабилометрический модуль деформации»). Отметим, что для конструкционных материалов (металл, бетон и т.п.) эта проблема пока не является актуальной, поскольку при действующем сейчас уровне напряжений в конструкциях из этих материалов влияние напряжений на их жесткость очень мало, хотя многие эффекты, которые имеют существенное значение для грунтов, впервые были подмечены для металлов, например, влияние вида нагружения, характеризуемого параметром Лоде-Надаи µs, что является главной причиной различия величин модуля деформации по данным испытания грунта штампами и прессиометром. Понятно, что применение для разных по пропорциям различных типов деформаций величин поправочно-переходных коэффициентов (например, коэффициента mk перехода от компрессионного модуля Ek к полевому модулю E в Пособии [11] или коэффициента Kr перехода от прессиометрического модуля Eпр. к полевому модулю E в ГОСТ 20276-99) достаточно противоречиво, особенно когда на компрессионный коэффициент mk накладывается еще и нарушение природного состояния грунта. Если все-таки, при логичном обосновании необходимо получить примерное соотношение между величинами модулей из разных типов испытаний, то эти коэффициенты должны быть узколокальными (только для данного грунта и для данной, в лучшем случае, местности). Трудности возникают и при расчете деформаций грунтов и напряженного состояния в них. Можно указать на достаточно противоречивое, неоднократно изменявшееся в нормативных документах условие ограничения сжимаемой толщи, на чрезмерное расчетное влияние строящихся сооружений на существующие объекты при расчетах в рамках линейной теории Гука и в то же время на заниженное это влияние в рамках линейной теории Фусса (способ корректировки этого влияния в рамках линейных теорий не разработан). Имеется и существенное расхождение фактических и расчетных значений контактных напряжений под фундаментами (см. рис.4), особенно под плитными фундаментами. Все эти проблемы являются следствием противоречия применения к физически и геометрически нелинейной грунтовой среде линейных соотношений Гука-Юнга-Пуассона. Особенно это касается принятия для грунта по аналогии с конструкционными материалами модуля Юнга E (модуля деформации в качестве грунтовой константы, хотя хорошо, например, известно, что при штамповых и прессиометрических испытаниях на разных глубинах даже в однородном грунте величина модуля с глубиной возрастает [6]. Для преодоления этого кажущегося противоречия в ГОСТ 20276-99 даже рекомендуется уменьшающийся с глубиной поправочный коэффициент KP, что на самом деле по сути придает грунту статус резины или металла с постоянным модулем Юнга. Немаловажен при этом, вытекающий из соотношений (1 и 2) факт зависимости от напряжений и коэффициента Пуассона n, который вопреки этому используется в качестве константы в формулах ГОСТ 20276-99 и ГОСТ 12248-2010 для вычисления модуля деформации E. В результате складывается ситуация при которой, по сути, в инженерно-геологических отчетах проектировщикам выдается недостоверная справка о деформационных параметрах нескальных грунтов Кстати, приближенная зависимость для модуля деформации, полученная с учетом физической нелинейности грунта из соотношений (1 и 2) и в которую не входит противоречивый для грунта (хотя бы из-за влияния на него эффекта дилатансии-контракции) коэффициент Пуассона свидетельствует как раз о возрастании модуля деформации E с увеличением глубины h:
- gn – нормативное значение удельного веса испытываемого грунта; An и Cn – нормативные значения параметров прочности Мизеса-Боткина.
- что средством преодоления проблем и противоречий, связанных с использованием в расчетах грунтовых оснований и грунтовых сооружений моделей линейно-деформируемой среды является применение в расчетах моделей, отражающих физически нелинейный характер деформирования, а возможно и другие существенные особенности грунтовой среды (геометрическую нелинейность и реологические свойства). Конечно должна быть учтена прежде всего главная особенность грунтов – их природное происхождение. Для этого параметры нелинейных моделей грунта должны определяться в условиях его естественного состояния, т.е. из данных полевых (in-situ) испытаний, иначе, как показывают исследования [4], ошибка при применении в расчетах с использованием нелинейных моделей данных лабораторных испытаний достигает 100%, правда в сторону завышения расчетной деформативности грунта, но при этом возникают и другие важные вопросы, связанные, например, с распределением и перераспределением напряжений в грунтах, в частности в песке. Возникают также еще почти непреодолимые трудности и с учетом в лабораторных испытаниях геометрической нелинейности. При этом в случае определения параметров деформирования линейных моделей эта ошибка может достигать 600 и более %, (например, в виде различия величин полевого и компрессионного модулей), в том числе и из-за неопределенности величины параметра n. Для базового варианта нелинейной модели Боткина вместо четырех констант E, n, j, c моделей Гука-Юнга и Кулона, необходимо определять пять параметров, входящих в формулы (2): Ао,
, А, В, С т.е. всего на один параметр больше, чем для комплекса линейных моделей, причем, как отмечалось выше, внутри линейной модели Гука-Юнга достоверного способа определения коэффициента Пуассона n по данным полевых (in-situ) испытаний не существует, что является еще одной проблемой при использовании моделей линейного деформирования грунта. К тому же феноменологические нелинейные зависимости модели Боткина являются обобщающими зависимостями также феноменологических, но линейных зависимостей (моделей) Гука-Юнга и Кулона, причем физически объективно, с точки зрения механизма деформирования грунта – связь деформации с прочностью – нелинейные модели в отличие от линейных их объединяют. Метод определения параметров нелинейной модели Боткина по данных испытаний грунта штампом и прессиометром приведен в [12]. Главной особенностью полевых схем испытаний грунтов является ограниченный набор измеряемых величин: как в прессиометрическом, так и штамповом испытаниях измеряется одно из трех возможных в пространстве перемещений и одно из трех главных напряжений, представленных давлением на грунт. При этом в испытании штампом это давление фиксируется приближенно, поскольку распределение контактного давления под штампом крайне неравномерно и к тому же зависит от уровня нагрузки на штамп (см. рис. 4). Направление же передачи нагрузки на грунт, т.е. схема испытания определяет особенности пространственного распределения напряжений и деформаций в испытуемом массиве и учитывается в нелинейных моделях, упоминавшимся выше параметром вида напряженного состояния µs, равным +1 вокруг радиального прессиометра и -1 под круглым штампом. Влияет этот параметр главным образом на деформации формоизменения. т.е. на модуль сдвига G, который, в свою очередь, зависит от констант А,В,С. Влияние вида напряженного состояния на изменение объема при эффекте дилатансии-контракции также существует, но главная его компонента при использовании данных полевых испытаний учитывается величиной параметра Ао. Наиболее точно влияние параметра µs, можно зафиксировать при проведении параллельных прессиометрического и штампового испытаний. Согласно формулам Малышева [10]:
- параметра вида напряженного состояния µs (в формуле 4 он для простоты обозначен µ) на величины параметров A, C одинаково и не превышает обычно 50%, о чем свидетельствуют также экспериментальные исследования [4] Влияние параметра µs на величину параметра можно определить по соотношению перемещений грунта при одном и том же давлении на грунт в прессиометрическом и штамповом испытаниях по правилам теории ошибок, имея в виду вид формулы (2). Вместе с тем, в случае невозможности проведения параллельных испытаний, параметра µs на величину параметра может быть достоверно определено другими методами, один из которых является следствием подобия реальных и численно смоделированных графиков деформации грунта при прессиометрическом и штамповом нагружении. Основной же проблемой при определении параметров нелинейной модели по данным полевых испытаний, как указывалось выше, является ограниченный набор измеряемых величин при не очень простых, определяющих деформацию соотношениях, например, типа (2). Это обстоятельство сводит задачу определения параметров грунта к решению, так называемой обратной некорректной, т.е. плохо обусловленной задачи, требующей для получения однозначного и физически корректного результата применения определенных регулязирующих процедур, учитывающих особенности конкретной проблемы [13].
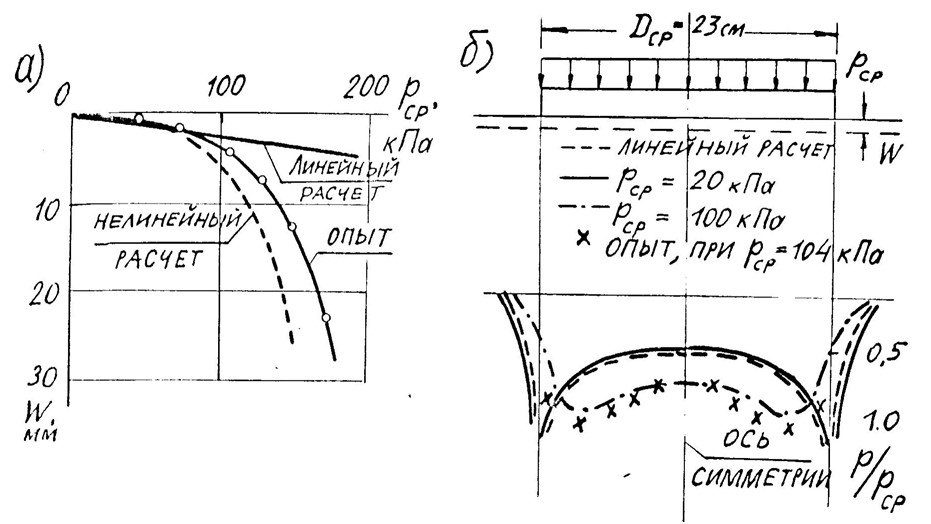
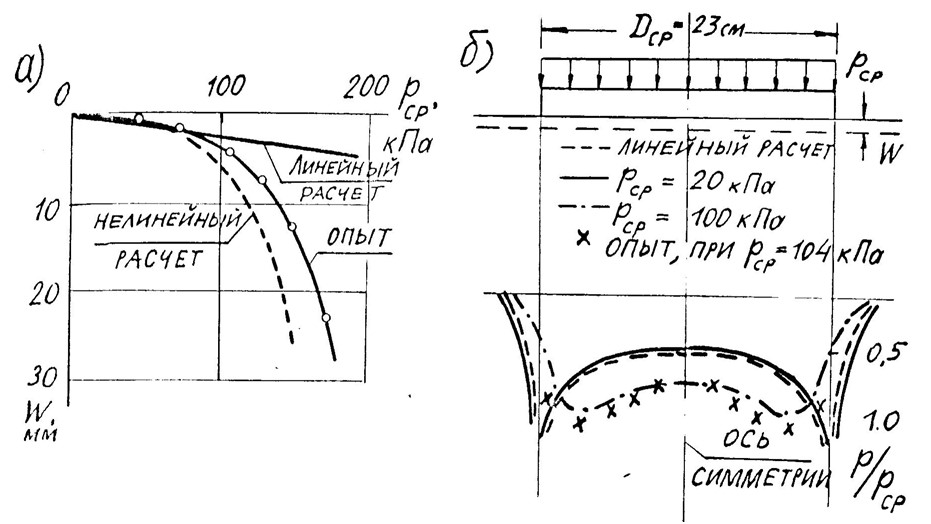
Рис.4. Результаты линейного и нелинейного расчетов [1]: а) графики осадки круглого жесткого фундамента и штампа; б) эпюры контактных напряжений под круглым жестким фундаментом и штампом
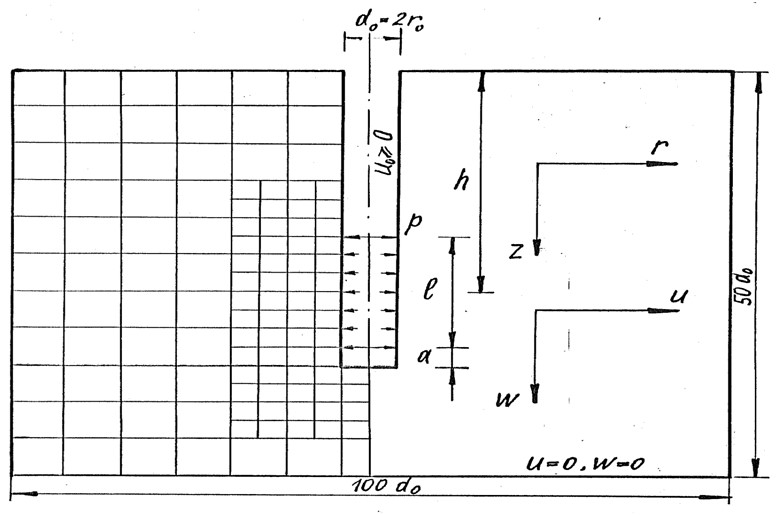
Рис.5. Расчетная схема двумерной осесимметричной задачи из [4]
- [12] изложен, как сам алгоритм метода определения параметров, так и обоснованы существование и единственность физически корректного результата. Основным принципом метода является комплексное использование результатов полевых и лабораторных испытаний грунта, а также результатов численного моделирования его деформаций при статических испытаниях штампами и радиальным прессиометром с использованием двумерных осесимметричных схем (см. рис.5). Одной из центральных позиций алгоритма является использование подобия фактических и численно смоделированных графиков деформации грунта для определения величины ключевого параметра B модели Боткина, в первую очередь определяющего форму графиков сдвиговой деформации в осях (si - ei), а поскольку сдвиговая компонента превалирует в деформации грунта, то этот параметр определяет и форму интегральной кривой осадки штампа и перемещения стенки скважины в прессиометрическом испытании. алгоритме также использована важная особенность грунта – ограниченный, но при этом достаточно широкий дискретный, с практически значимым интервалом через 10 диапазон одного из главных параметров грунта – его угла внутреннего трения j. Для решения используемой в алгоритме прямой двумерной осесимметричной задачи, расчетная схема которой приведена на рисунке 5, применена эффективная, малозатратная по ресурсам ЭМ модификация метода Зейделя с ускоряющей процедурой Рунге-Ромберга [14], что позволяет использовать для применения метода современные персональные компьютеры широко доступной мощности. При этом в численной реализации через стандартные геометрические соотношения [15] учтена и геометрическая нелинейность, а проведение испытаний грунта с соблюдением принципа условной стабилизации деформаций обеспечивает учет его реологических свойств. Применение в практических расчетах моделей грунта, учитывающих особенности его нелинейного деформирования, с использованием значений параметров из результатов полевых испытаний, позволило авторам решить ряд нерешаемых в рамках линейной теории практических вопросов: для ряда объектов в городе Екатеринбурге и в Свердловской области была оценена реальная жесткость грунтов основания с определением степени увеличения ее с глубиной, что позволило в одних случаях увеличить этажность зданий, в других случаях уточнить влияние строящихся высотных зданий на существующие сооружения, в третьих случаях обеспечить строительство зданий на относительно слабых грунтах и на искусственных основаниях. Во всех случаях фактические результаты с необходимой точностью совпали с расчетными прогнозами. В качестве характерного примера можно привести полное отсутствие недопустимых деформаций (в виде трещин) в двух существующих зданиях 1960-ых годов постройки после возведения между ними в 2000-м году нового здания-вставки, хотя по прогнозам проектировщиков на основе линейной теории трещины в них неизбежно должны были возникнуть. В другом случае были отменены рекомендации проектировщиков по дорогостоящему укреплению грунтов основания здания медицинского центра перед его реконструкцией. Оценка жесткости основания на основе нелинейной модели Боткина выполнялась с помощью автоматического прессиометра ПЭВ-89-МК. На рис. 6 приведены результаты оценки фактической жесткости грунта основания проектируемого здания школы в городе Серове Свердловской области
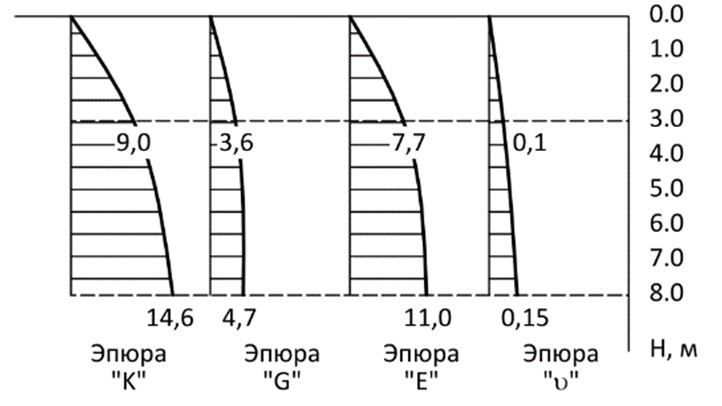
- Пример увеличения жесткости мягкопластичной (IL » 0,64) высокопористой (e »1,5 палеогеновой глины: с увеличением глубины на 5 м жесткость грунта увеличилась почти в 1,5 раза
Выводы
- Для расчетов деформаций грунтов следует применять модели и расчетные схемы, отражающие физическую и геометрическую нелинейность; при этом следует избегать использования моделей, в определяющих соотношениях которых используются проблемные для определения в грунтах модуль Юнга E и коэффициент Пуассона n.
- Параметры нелинейных моделей должны определяться из результатов полевых испытаний, поскольку использование лабораторных данных вследствие неизбежного нарушения природного, прежде всего, напряженного состояния грунта приводит, как минимум к 100% ошибке в результатах
- Наиболее удобными для определения параметров нелинейных моделей грунтов являются приборы, обеспечивающие двухмерную осесимметричную схему нагружения (радиальные прессиометры и плоские штампы); при этом прессиометр может иметь длину, а штамп диаметр, меньшие, чем при определении параметров линейной модели, что, с одной стороны позволяет обеспечить более высокий уровень давления на грунт, а с другой стороны учитывается расчетной схемой, в которой, что также немаловажно для грунта, довольно легко и адекватно учитывается фактор геометрической нелинейности.
1. Соломин В.И., Шматков С.Б. Об учете нелинейных деформаций железобетона и грунта при расчете круглых фундаментных плит // Основания, фундаменты и механика грунтов. - 1976. - №3. - С. 36-39.
2. Копейкин В.С., Соломин В.И. Расчет песчаного основания с помощью физически и геометрически нелинейных уравнений // Основания, фундаменты и механика грунтов. - 1977. - №1. - С. 30-32.
3. Бугров А.К. Расчеты грунтовых оснований при развитии в них областей предельного напряженного состояния. - В кн.: Экспериментально-теоретическое исследования нелинейных задач в области оснований и фундаментов. Межвузовский сборник. - Новочеркасск, изд. НПИ, 1979. - С. 65-71.
4. Алехин А.Н. Нелинейный анализ напряженно- деформированного состояния грунтовых массивов при статическом нагружении: Дисс. канд. техн. наук/ Уральский политехнический институт. Свердловск, 1982. - 186 с.
5. Ухов С.Б., Семенов, В.В. Знаменский В.В., Тер-Мартиросян З.Г., Чернышев С.Н. Механика грунтов, основания и фундаменты / Учебное пособие: - М.: Высшая школа, 2002. - 566 с.
6. Клейн Г.К. Учет неоднородности, разрывности деформаций и других механических свойств грунтов при расчете сооружений на сплошном основании. - В кн.: Сб. трудов МИСИ им. В.В. Куйбышева, №14. - М.: Госстройздат, 1956, С. 168-180.
7. Лушников В.В., Алехин А.Н. Оценка достоверности определения модуля деформации по данным испытаний грунтов // Устройство оснований и фундаментов в слабых и мерзлых грунтах: Межвузовский тематический сб. трудов. - Л.: ЛИСИ, 1982. - С. 53-60.
8. Боткин А.И. Исследование напряженного состояния в сыпучих и связных грунтах // Известия НИИГ, том 26, 1940., С. 205-236.
9. Kriegel H.J., Wiesner H.H. Problems of Stress-Strain Conditions in Subsoil: Proceedings of VIII-th ICSMFE, Moscow, 1973, tom1.3, pp.133-141.
10. Малышев М. В. Прочность грунтов и устойчивость оснований сооружений. - М.: Стройиздат, 1994. - 227 с.
11. Пособие по проектированию оснований зданий и сооружений (к СНиП 2.02.01-83). - М.: НИИОСП Госстроя СССР, 1986. - 415 с.
12. Алехин А.Н. Обоснование метода определения параметров нелинейной модели грунта по данным его полевых испытаний // Академический вестник УралНИИпроект РААСН - Екатеринбург: УралНИИпроект, 2015. - №1. - С. 57 - 62.
13. Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. М.: Наука, 1979. - 285 с.
14. Калиткин Н.Н. Численные методы. М.: Наука, 1978. - 512 с.
15. Новожилов В.В. Теория упругости. Л.: Судпромгиз, 1958. - 370 с.
