с 01.01.1998 по настоящее время
Россия
с 01.01.1965 по настоящее время
Россия
с 01.01.2015 по 01.01.2019
ББК 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
: Разработать рекомендации по применению полимербетонных изгибаемых конструкций невозможно без создания или оптимизации существующих методов расчета, особенно это актуально для изгибаемых элементов, в которых применяется разноуровневое армирование. Для применения (особенно в условиях воздействия агрессивных сред) в качестве материала изготовления изгибаемых конструкций нами предлагается каучуковый бетон - полимербетон, которому свойственны высокие прочностные характеристики. Важно отметить, что в составе фиброкаутона применяются отходы промышленного производства, такие как зола-унос и волокна металлокорда. Балки из каутона и фиброкаутона были испытаны на чистый изгиб – наиболее характерный вид нагружения при изучении таких элементов. В результате проведенных теоретических исследований полимербетонных балок были установлены предпосылки для расчета по первой группе предельных состояний каутоновых и оптимизирована методика расчета фиброкаутоновых балок. Определено, что фибровое армирование с процентом армирования по массе каутонового элемента равное 2,5% соответствует работе стержневого продольного армирования со значением μ=0,34%.
каутон, фибра, фиброкаутон, балка, нормальные сечения, прямоугольное сечение, изгибаемый элемент, прочность.
Применение полимербетонов наиболее актуально в изделиях или элементах, эксплуатируемых в условиях воздействия агрессивной среды различного типа. Каучуковый бетон или сокращенно каутон – полимербетон, обладающий практически универсальной химической стойкостью и высокой прочностью на основе жидких каучуков. Применение каутона в конструкциях на данный момент ограничено отсутствием рекомендации по их проектированию и расчета. Исходя из анализа работ [1-6], а так же из анализа нормативной литературы можно сказать, что на прочность нормальных сечений, в большей степени влияет площадь стержневого армирования. В работах [7,8] установлено, что фибра также вносит свой вклад в работу сечений изгибаемых элементов, а в работах [9,10] была установлена степень влияние дисперсного армирования из различного вида волокон на прочностные характеристики каутона. Исследования, проведённые в работе [11] подтверждают положительное влияние стальной фибры, введенной в состав обычного бетона, на прочностные характеристики материала.
В результате экспериментальных исследований изложенных в статье [8] и проведенного анализа нормативной литературы были определены предпосылки метода расчета прочности нормальных сечений каутоновых изгибаемых элементов без дисперсного армирования:
1. Расчет производится в момент разрушения образца.
2. Растягивающие усилия воспринимает арматурный стержень.
3. Значения напряжений в материале сжатой зоны достигают предела прочности, независимо от того по какой зоне разрушается материал.
Несущую способность определяем согласно уравнениям равновесия изгибающих моментов относительно центра тяжести сечения растянутой арматуры:
![]()
где x – высота сжатой зоны,
Rk – предел прочности каутона на сжатие,
b – ширина сечения;
Высота сжатой зоны определяется из суммы проекций внутренних усилий на продольную ось элемента.
Для каутоновых изгибаемых элементов без дисперсного армирования:
![]()
где Rs – расчетное сопротивление арматуры. Стоит отметить, что в материалах статьи вместо Rs применялся σt – экспериментальный предел текучести для обеспечения сходимости расчетных значений с экспериментальными, т.к. за разрушающую нагрузку во время испытаний принималась та, при которой арматурной сталью достигается предел текучести.
As – площадь стержневой арматуры;
Результаты расчета по приведенной методике приведены в таблице 1.
Таблица 1
Экспериментальные и расчетные значения прочности нормальных сечений каутоновых изгибаемых элементов
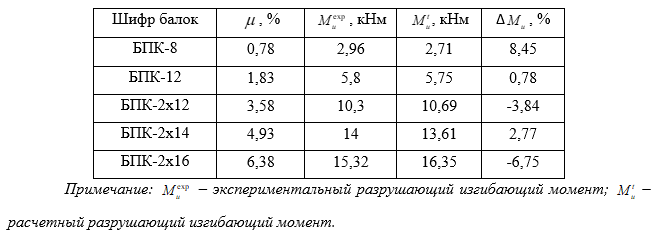
Из таблицы 1 видно, что “стандартная” методика расчета прочности нормальных сечений балок (согласно СП 63.13330.2012), обеспечивает достаточную сходимость результатов расчета с экспериментальными значениями.
Однако расчет по приведенной выше методики для фиброкаутоновых элементов не обеспечивает должной сходимости, что говорит о необходимости учета работы фибровых волокон в трещине в процессе их развития. С целью определить степень влияния фибровых волокон на прочность нормальных сечений нами были изготовлены 2 серии балок без стержневого армирования, изготовленные из каутона и фиброкаутона, результаты, испытания которых приведены в таблице 2.
Таблица 2
Экспериментальные значения прочности нормальных сечений каутоновых изгибаемых элементов без стержневого армирования
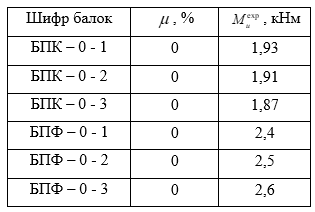
На основании данных полученных в таблицах 1 и 2 были построены графики (рисунок 1) зависимости изгибающего разрушающего момента от процента продольного армирования для балок без стержневого армирования и для балок армированных одним стержнем диаметров 8 мм.
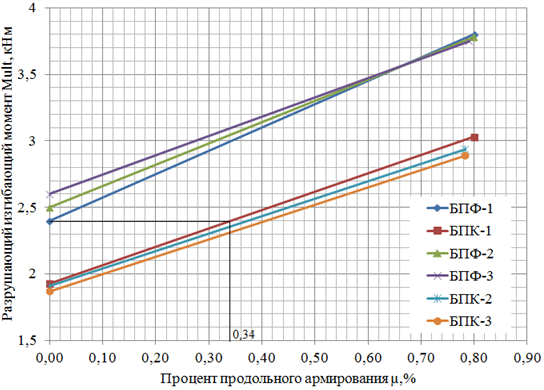
Рис.1. Графики зависимости изгибающего момента от процента продольного армирования
Как можно увидеть эквивалентный процент продольного стержневого армирования, учитывающий работу волокон металлокорда в нормальных сечениях равен ~0.34%. Данное значение μ соответствует 2,5 % дисперсного армирования от массы элемента. Следовательно, для фиброкаутоновых изгибаемых элементов можно учесть влияние дисперсного армирования при расчете по первой группе предельных состояний путем добавления эквивалентной дисперсному стержневой площади армирования к площади продольного армирования:
![]()
где Rfk – предел прочности фиброкаутона на сжатие.
Результаты расчета прочности фиброкаутоновых элементов по оптимизированной методике в сравнение с экспериментальными результатами приведены в таблице 3.
Таблица 3
Экспериментальные и расчетные значения прочности нормальных сечений фиброкаутоновых изгибаемых элементов
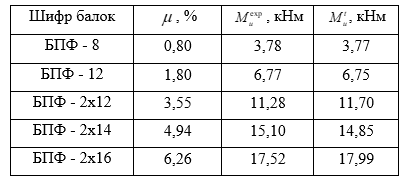
Очевидно, что подобный способ учета фибрового армирования при расчете обеспечил достаточную сходимость расчетных значений разрушающего изгибающего момента с экспериментальными значениями
Выводы и рекомендации
Установлены предпосылки для расчета фиброкаутоновых изгибаемых элементов. Определено, что фибровое армирование с процентом армирования по массе каутонового элемента равное 2,5% соответствует работе стержневого продольного армирования со значением μ=0,34%. Оптимизирована методика расчета по первой группе предельных состояний, изложенная в СП, для обеспечения необходимой сходимости результатов расчета с экспериментальными значениями.
1. Нгуен Фан Зуй. Двухслойные каутоно-бетонные изгибаемые элементы строительных конструкций: дис. … канд. техн. наук. Воронеж, 2010. - 185 с.
2. Борисов Ю.М., Поликутин А. Э., Нгуен Фан Зуй Напряженно-деформированное состояние нормальных сечений двухслойных каутоно-бетонных изгибаемых элементов строительных конструкций // Научный вестник ВГАС «Архитектура и строительство». Воронеж, 2010. № 2. С. 18-24.
3. Пинаев С.А., Франсиско Савити Матиас Да Фонсека, Влияние полимерцементной защиты на трещиностойкость железобетонных изгибаемых элементов / Научный вестник Воронежского государственного архитектурно-строительного университета // Материалы межрегиональной научно-практической конференции "Высокие технологии в экологии", 2011. №9. С. 85-88.
4. Пинаев С.А. Короткие сжатые элементы строительных конструкций из эффективного композита на основе бутадиенового полимера: дис. … канд. техн. Наук. Воронеж, 2001. - 191 с.
5. Potapov Y. B., Pinaev S. A., Arakelyan A. A., Barabash A. D. Polymer-cement material for corrosion protection of reinforced concrete elements, Solid state phenomena. 2016. №871. P. 104 - 109.
6. Potapov Y., Polikutin A., Panfilov D., Okunev M. Comparative analysis of strength and crack resistance of normal sections of bent elements of T-sections, made of rubber concrete, cauton reinforcement and concrete // MATEC Web of Conferences. 2016. №73. https://doi.org/10.1051/matecconf/20167304018
7. Панфилов Д.В. Дисперсно армированные строительные композиты на основе полибутадиенового олигомера: дис. ... канд. техн. наук. Воронеж, 2004. 188 c.
8. Поликутин А.Э., Потапов Ю.Б., Левченко А.В. Экспериментальные исследования влияния дисперсного армирования на прочность нормальных сечений изгибаемых элементов из каутона // Известия высших учебных заведений. Строительство. Новосибирск, 2018. №8. С. 28-35
9. Корнеев А.М., Бузина О.П., Суханов А.В. Детерминированная математическая модель и алгоритм анализа напряженно-деформированного состояния изгибаемых элементов с дискретными волокнами // Современные наукоемкие технологии № 9, - 2016 - С. 57-62.
10. Song, P. S. Mechanical properties of high-strength steel fiber-reinforced concrete / P. S. Song, S. H. Wang // Construction and Building Materials, Vol. 18 -2004 - Issue 9 - P. 669-673.
11. Борисов Ю.М., Панфилов Д.В., Каштанов С.В., Юдин Е.М. Дисперсно-армированные строительные композиты / Строительная механика и конструкции, 2010. № 2 (5). С. 32-37.


















