с 01.01.2019 по настоящее время
Архангельск, Архангельская область, Россия
Архангельск, Архангельская область, Россия
УДК 62 Инженерное дело. Техника в целом. Транспорт
ГРНТИ 67.21 Инженерные изыскания в строительстве
ГРНТИ 67.01 Общие вопросы строительства
ОКСО 08.06.01 Техника и технологии строительства
ББК 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
Ряд авторов обращают внимание на феномен, связанный с почти двукратным увеличением коэффициента вторичной консолидации торфа в ходе компрессионных испытаний. Длительные лабораторные эксперименты показали, что это явление обусловлено не природой процессов, происходящих в торфе, а несоответствием логарифмической зависимости экспериментальным данным. Для прогноза осадки торфа может применяться степенная зависимость деформации от времени.
торф, компрессионные испытания, вторичная консолидация
Введение
В условиях естественного залегания 90-95 % объема торфа составляют заполненные водой поры, оставшийся объем занят растительными остатками различной степени разложения и небольшим количеством минеральных частиц. Как показывают лабораторные и полевые эксперименты, при нагрузке до 100 -150 кПа первичная или фильтрационная консолидация торфа завершается при весьма высоких значениях коэффициента пористости, как правило, от 6 до 11 [5]. Вполне очевидно, что такую нагрузку воспринимают не сами растительные остатки, а сорбированная ими поровая влага. Об этом свидетельствует, в частности, сохраняющаяся после завершения компрессионных испытаний способность образцов торфа к усадке.
Многие авторы обращали внимание на необычное поведение торфа при компрессии с весьма непродолжительным процессом первичной консолидации и растянутым во времени этапом вторичной консолидации [10, 16]. По данным L.S. Wong, R. Hashim, F.H. Ali [16], A.W. Dhowian and T.B. Edil [9] и других авторов фильтрационная консолидация торфа в одометрах завершается в течение нескольких минут или нескольких часов. Эта особенность объясняется двухуровневой структурой торфа, а именно, наличием крупных растительных остатков с закрытыми микропорами, каналами и расположенных в макропорах между ними мелких частиц и волокон [12, 18]. Первичная консолидация обусловлена удалением свободной воды из макропор, а вторичная - связанной влаги из микропор и каналов. О том, что переход от первичной ко вторичной консолидации торфа обусловлен началом удаления из его пор связанной влаги, писал и Л.С. Амарян [1]. Л.Е. Мальцев и А.П. Малышкин отмечали, что в слабых водонасыщенных заторфованных грунтах защемленная в порах вода способна воспринимать 60-90 % внешней нагрузки [4].
Многочисленные полевые и лабораторные эксперименты показали, что, так называемое, поровое давление рассеивается гораздо раньше, чем возникает перегиб на графике зависимости осадки от логарифма времени s = f(lgt) - точка Р на рис. 1, по которому и определяют переход от первичной ко вторичной консолидации [7, 16]. По мнению З.Г. Тер-Мартиросяна для высокодисперсных грунтов вообще не следует разделять напряжения между скелетом и поровой влагой, а измеряемое в экспериментах поровое давление есть разность между внешним и расклинивающим давлением пленок связанной влаги [6].
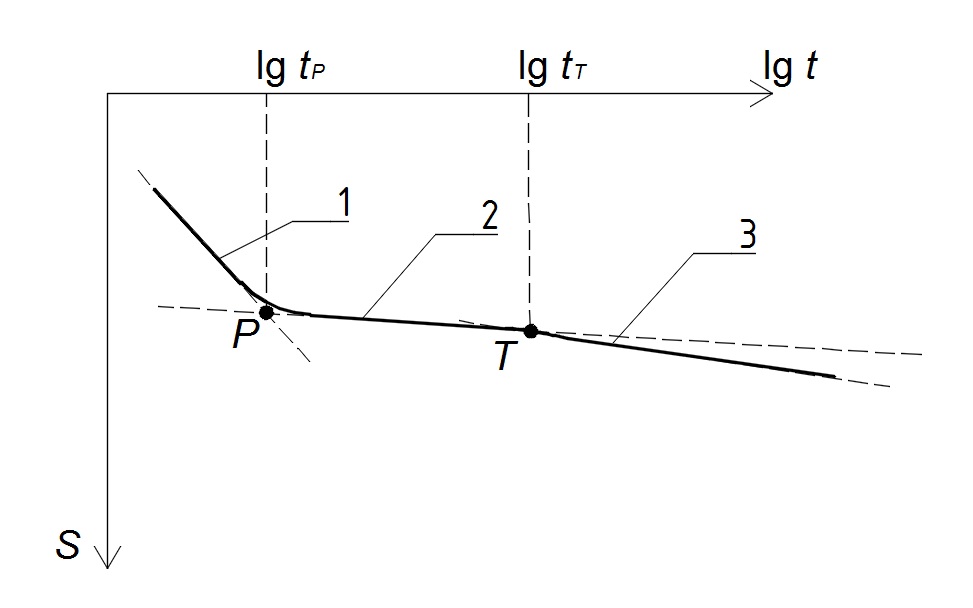
Рис. 1. Развитие деформаций торфа во времени при компрессионных испытаниях:
1 - первичная, 2 - вторичная, 3 - третичная консолидация
В 1979 г. A.W. Dhowian и T.B. Edil [8] обратили внимание, что у графиков s = f(lgt), полученных по результатам двухмесячных компрессионных испытаний торфа, на участке вторичной консолидации имеется излом – точка Т на рис. 1. Они назвали явление, связанное с третьим участком графика, третичной консолидацией. По данным E. Yilmaz и A. Saglamer [17] время перехода в стадию третичной консолидации может быть найдено по формуле lg tT = (lg tP + 2), где tP - время завершения первичной консолидации.
О феномене третичной консолидации упоминали многие ученые. B.C. O'Kelly [14] считал причиной этого явления разложение органического вещества, а E. Malinowska [13] интерпретировала его как переход в стадию прогрессирующей ползучести. Наличие перегиба на ветви вторичной консолидации можно заметить и на приведенных В.Н. Брониным [2] графиках длительных компрессионных испытаний торфа при давлении 40-160 кПа. По мнению H. Brandl [7] стадия третичной консолидации связана, наоборот, с угасанием темпа осадки образцов.
Рассматриваемый, казалось бы, весьма специфический частный вопрос интерпретации данных компрессионных испытаний торфа имеет большое практическое значение, так как коэффициент вторичной консолидации используется для прогноза длительной осадки торфа, а, учитывая высокую сжимаемость этого грунта, ошибки в прогнозе чреваты появлением дефектов на дорогах, тротуарах, в полах промышленных зданий, элементах благоустройства и коммуникациях. В частности, в г. Архангельске, построенном на заболоченной равнине, вопреки прогнозам, осадка торфа под слоем техногенных отложений не завершается уже в течение нескольких десятилетий (рис. 2) [5, 15].
Рис. 2. Повреждение покрытия тротуара из-за неравномерной осадки торфа в основании
Материалы и методы исследований
В настоящей статье представлены результаты длительных компрессионных испытаний торфа. Опыты проводились с низинным торфом средней степени разложения (Dpd = 40-45 %). Образцы ненарушенной структуры отбирались в окрестностях г. Архангельска на неосвоенном, неосушенном болоте из шурфов с глубины 0,5-0,8 м. Исходные свойства торфа: плотность 0,98-1,12 г/см3, плотность частиц 1,44-1,45 г/см3, влажность весовая 770-1060 %, коэффициент пористости 11,8-13,8. Фотография структуры торфа, выполненная на сканирующем электронном микроскопе Vegan Tescan 3 с увеличением в 500нм, представлена на рис. 3.
Рис.3. Структура исследуемого торфа
Испытания проводились в компрессионно-фильтрационных приборах в течение 6 месяцев. Площадь поперечного сечения образцов составляла 60 см2, высота 3, 5 и 7 см. Нагрузка прикладывалась сразу в одну ступень, как того требуют нормативные документы при определении коэффициента консолидации. Полости под нижним пористым диском заполнялись водой и соединялись с бюретками, служившими для определения коэффициента фильтрации. Приборы размещались в помещении с температурой 5-12°С, что замедляло разложение органического вещества торфа.
До начала компрессионного сжатия коэффициент фильтрации образцов k был равен 0,018 - 0,129 м/сут при среднем значении = 0,061 м/сут. В последующем водопроницаемость торфа определялась периодически по мере деформирования образцов.
Испытания на консолидацию были проведены на 9 образцах - по три образца высотой 3, 5 и 7 см при трех значениях давления - 25, 50 и 100 кПа. Завершились испытания определением силы трения между образцами и рабочим кольцом. Для этого в специальной загрузочной раме замерялось усилие, необходимое для выдавливания образцов из кольца.
Результаты экспериментов
В геотехническом проектировании распространено два способа обработки данных компрессионных испытаний и расчета осадки основания. В первом из них компрессионную зависимость строят с использованием конечных значений относительной деформации ε или коэффициента пористости образцов e, полученных при достижении условной стабилизации, спрямляют эту зависимость в заданном интервале давления p, находят модуль деформации E, который и используют для расчета конечной осадки. Во втором способе, принятом в зарубежной практике, компрессионную зависимость строят на момент завершения первичной или фильтрационной консолидации, спрямляют ее в координатах ε – lgp или e – lgp и находят коэффициент компрессии cc, далее с помощью графика ε – lgt определяют коэффициент вторичной консолидации сα, а конечную осадку вычисляют как сумму мгновенной или упругой осадки, осадки при первичной и при вторичной консолидации грунта. Как отмечено выше, для торфа, возможно, следует принимать во внимание еще и третичную консолидацию, связанную с увеличением коэффициента сα в процессе деформирования образца.
На рис. 4,а представлены компрессионные кривые ε = f(p), построенные на момент завершения первичной консолидации (график 1) и на момент завершения опытов (график 2), где p – давление под поршнем компрессионного прибора. Оказалось, что деформации, произошедшие после завершения фильтрационной консолидации, весьма значительны – они составляют 15-30 % от конечных значений.
На рис. 4,б приведены те же зависимости, но с использованием значений напряжений в образце σ, найденных с учетом сил трения, действующих на контакте образца со стенками рабочего кольца. Оказалось, что такая корректировка привела к росту относительных деформаций образцов на 0,02-0,04 по сравнению с расчетом напряжений из условия σ = p. При мощности слоя торфа, например, 5 м это даст дополнительную осадку основания 10-20 см.
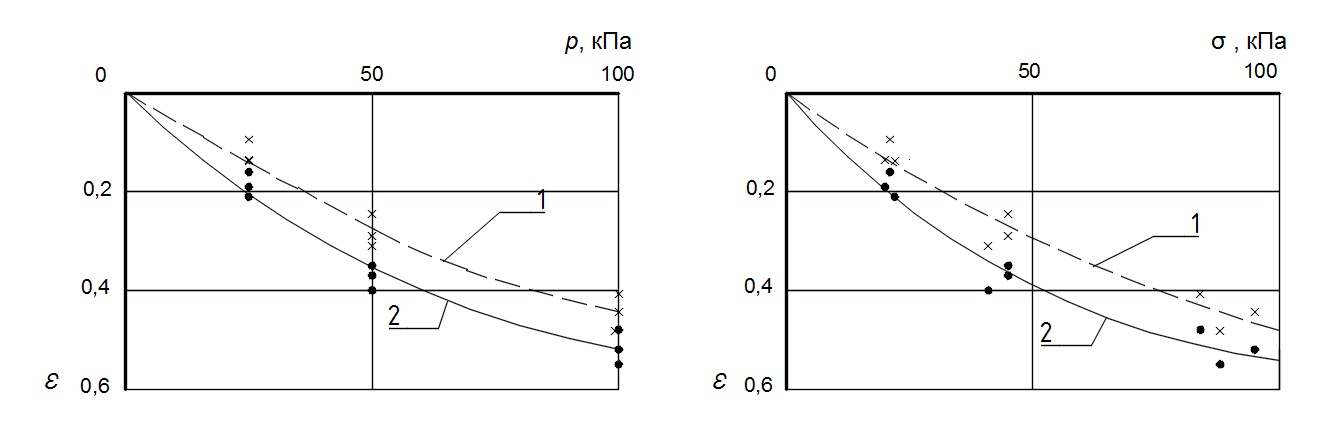
| а) |
б) |
Рис. 4. Зависимость относительных деформаций торфа ε: а) от давления под поршнем р,
б) от напряжений в образце σ; 1 – при завершении первичной консолидации,
2 – при завершении экспериментов
Зависимости, приведенные на рис. 4,б, при построении в полулогарифмических координатах становятся линейными (рис. 5). Коэффициент компрессии, найденный по формуле cc = Δε/Δlgσ на момент завершения фильтрационной консолидации, для исследуемого торфа составил 0,516.
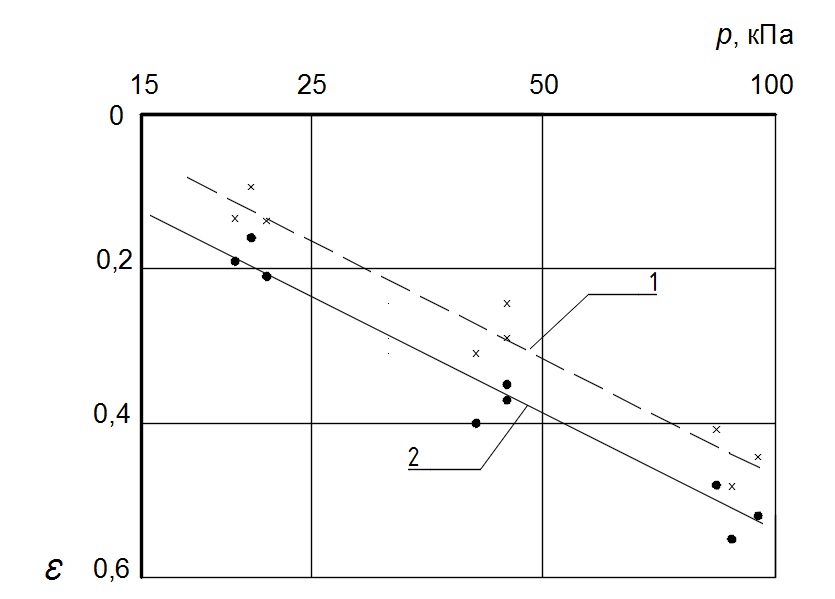
Рис. 5. Компрессионные зависимости торфа:
1 – при завершении первичной консолидации, 2 – при завершении экспериментов
Зависимость коэффициента фильтрации от коэффициента пористости приведена на рис. 6. Как видим, в результате компрессионного сжатия водопроницаемость торфа уменьшилась на три порядка. Весьма близкая зависимость была получена Л.С. Амаряном на торфе со степенью разложения Dpd = 20 % [1].
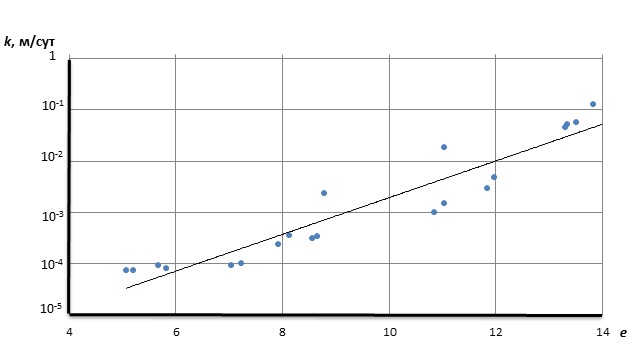
Рис. 6. Зависимость коэффициента фильтрации от коэффициента пористости
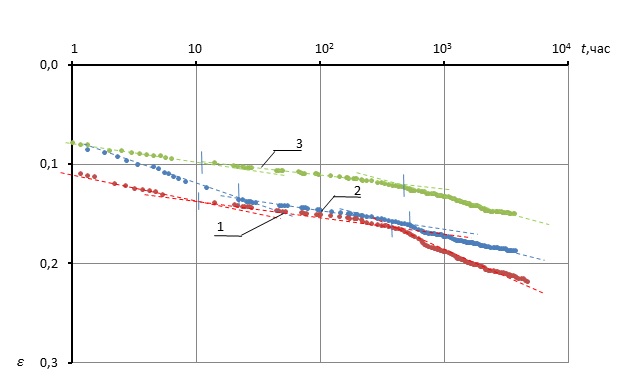
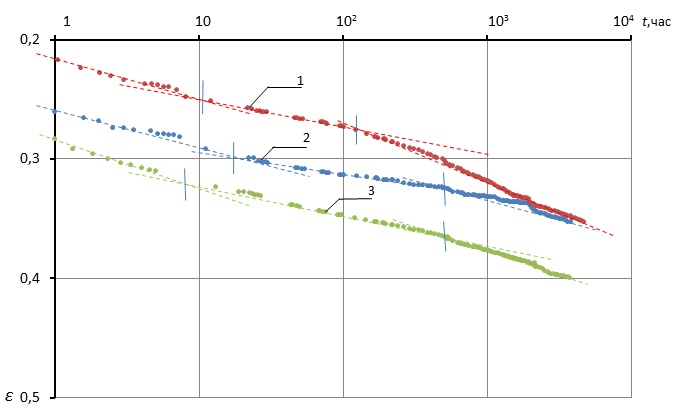
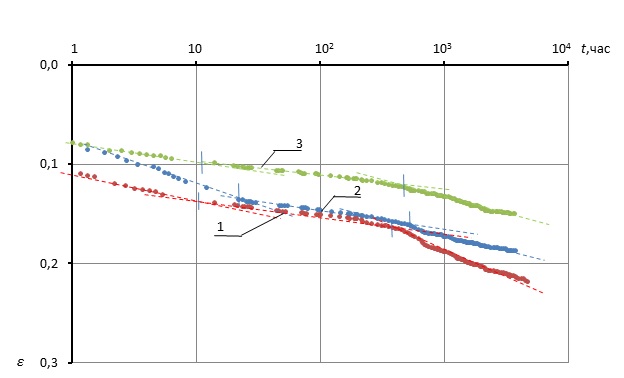
Теперь перейдем к анализу развития деформаций образцов во времени. На графиках зависимости относительных деформаций от времени, представленных на рис. 7, где использована логарифмическая шкала времени, действительно можно выделить три характерных прямолинейных участка. Коэффициент вторичной консолидации, равный тангенсу угла наклона второго прямолинейного участка графика к оси абсцисс, cα = Δε/Δlgt, изменяется от 0,013 до 0,027, его среднее значение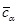 
= 0,021. Длина этого участка графика (lg tТ - lg tР) = 1,2-1,8, что несколько меньше значений, полученных E. Yilmaz и A. Saglamer [17].
а)
б)
в)
Рис. 7. Развитие деформации образцов торфа во времени:
а) σ = 20-23 кПа, б) σ = 45 -48 кПа, в) σ = 85-95 кПа
высота образцов: 1 – 3 см, 2 – 5 см, 3 – 7 см
На участке, так называемой, третичной консолидации наклон графика к оси абсцисс увеличился. Тангенс угла наклона, который для этого участка обозначим cαТ, достиг значений 0,027-0,053, среднее значение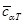 
= 0,037, что в 1,8 раза превышает 
.
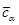Следует заметить, что, хотя наличие участка третичной консолидации и подтверждается экспериментально, но это явление связано не с природой процессов, происходящих в торфе при компрессии, а проявляется лишь благодаря использованию логарифмической шкалы времени. B.B.K.Huat и A.Prasad [11] применительно к коэффициенту вторичной консолидации cα справедливо заметили, что его постоянство говорит не о постоянстве, а о постепенном снижении скорости осадки. Сказанное относится и к, так называемой, третичной консолидации. Графики, представленные на рис. 8, показывают, что скорость развития относительных деформаций образцов dε/dt плавно снижается на стадиях как вторичной, так и третичной консолидации.
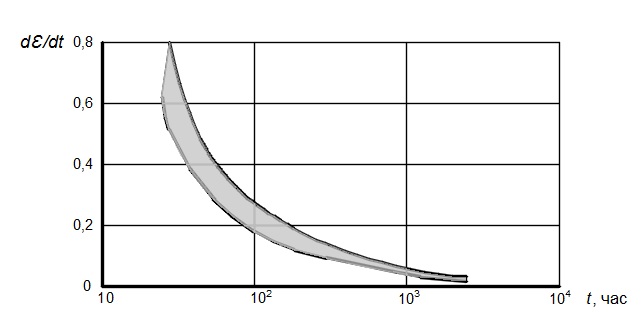
Рис. 8. Изменение скорости деформирования образцов во времени
Известно, что осадку основания за счет вторичной консолидации грунта основания за интервал времени Δt = (t2 - t1) находят по формуле [17]:
Ss = Δε H = cα H lg(t2/t1), (1)
где Н - толщина слоя грунта.
Использование двух коэффициентов консолидации - cα и cαT - усложняет расчет, тем более, что точка перехода от вторичной к третичной консолидации не имеет четкой привязки во времени.
Обработку данных компрессионных испытаний и вычисление осадки основания можно выполнять с использованием других зависимостей, в частности, степенной ε = btm или S =Hbtm [3, 5]. Параметры уравнений b и m можно находить путем спрямления экспериментальных зависимостей в логарифмических координатах lgε - lgt. В качестве примера такие графики на рис. 9 приведены для трех образцов торфа различной высоты, испытывавшихся при р = 100 кПа или σ = 85-95 кПа. Показатель степени m для них можно принять равным 0,024. Обработка данных экспериментов показала, что при σ = 20-23 кПа m = 0,072; при σ = 45-48 кПа m = 0,044.
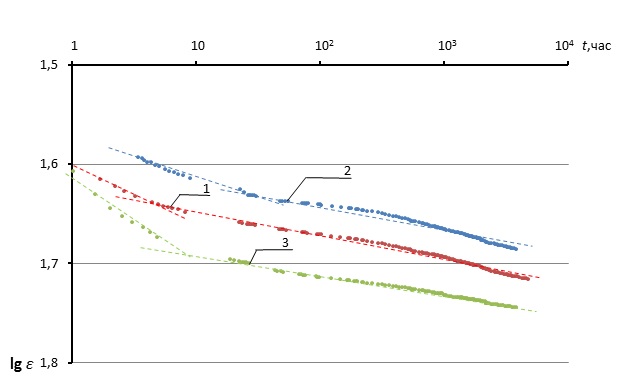
Рис. 9. Спрямление экспериментальных зависимостей ε = f(t)
в логарифмических координатах; высота образцов: 1 – 3 см, 2 – 5 см, 3 – 7 см
Проведя простые преобразования, получаем формулу для вычисления относительных деформаций торфа:
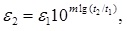(2)
где ε1 и ε2 - относительные деформации за время t1 и t2, прошедшее с момента приложения нагрузки.
Например, для одного из образцов торфа при σ = 95 кПа первичная консолидация завершилась при t1 = 13 часов, деформации составили ε1 = 0,450, а опыт закончился при t2 = 4678 часов. Отсюда расчетное значение относительных деформаций ε2 = 0,450·10 0,024 lg(4678/13) = 0,518. Если взять в качестве исходной одну из точек на участке вторичной консолидации, например, с координатами t1 = 52 часа, ε1 = 0,463, то расчетное значение конечных относительных деформаций составит ε2 = 0,463·10 0,024 lg(4678/52) = 0,516. Экспериментальное значение ε2 = 0,519. Таким образом, степенная зависимость вполне применима для прогноза деформаций торфа.
Осадку основания за счет вторичной (да и третичной) консолидации торфа можно найти следующим образом. Пусть за время, прошедшее с момента отсыпки насыпи, прошло 12 лет или 144 месяца, осадка достигла 270 cм. Лабораторные испытания образцов при напряжениях σ, равных нагрузке от насыпи, показали, что показатель степени m = 0,044. Тогда осадка за следующие 10 лет или 120 месяцев составит:
ΔS = 270(100,044 lg(264/144) - 1) = 7,3 см или 0,73 см/год.
Заметим, что по данным длительных наблюдений в г. Архангельске осадка поверхности из-за деформаций слоя торфа в основании протекает со скоростью 0,5-1 см/год [5].
Выводы:
1. На графиках зависимости относительных деформаций торфа от логарифма времени, построенных по результатам многомесячных компрессионных испытаний, действительно существует участок, называемый многими авторами третичной консолидацией, с наклоном к оси абсцисс, большим, чем при вторичной консолидации.
2. Наличие стадии третичной консолидации обусловлено не физическими процессами, развивающимися в слагающих торф растительных остатках или особыми свойствами удаляемой в ходе компрессионного сжатия сорбированной ими влаги, а всего лишь несоответствием применяемых зависимостей экспериментальным данным.
3. Для прогноза эмпирических осадок основания с успехом может применяться степенная зависимость с показателем степени, постоянным, как для стадии вторичной, так и третичной консолидации.
1. Амарян Л.С. Свойства слабых грунтов и методы их изучения. - М.: Недра, 1999. 220 с.
2. Бронин В.Н. Влияние ползучести и консолидации грунтов на напряженно-деформированное состояние основания при различных стадиях возведения сооруже-ния. СПб., 1993. 41с.
3. Вялов С.С. Реологические основы механики грунтов: Учеб.пособие для строи-тельных вузов. - М.:Высш.школа, 1978. 447 с.
4. Мальцев Л.Е., Малышкин А.П. Экспериментальное подтверждение кинематической модели грунта//Современные проблемы фундаментостроения: Сб.тр.междунар. научно-техн.конф. Ч.1,2/ ВолгГАСА. Волгоград, 2001, С.109-116.
5. Невзоров А.Л., Никитин А.В., Заручевных А.В. Город на болоте: монография. Архангельск: ИПЦ САФУ, 2012. 157 с.
6. Тер-Мартиросян З.Г. Реологические параметры грунтов и расчеты оснований сооружений. - М.: Стройиздат, 1990. 200 с.
7. Brandl H. Creeping (Secondary/Tertiary settlements) of highly compressible soils and sludge. Building materials and structures, 2018, V.61(1), p. 27-36.
8. Dhowian A.W., Edil T.B. Analysis of long-term compression of peats. Geotechnical Engineering, 1979, 10, p.159-178.
9. Dhowian A.W., Edil T.B. Consolidation behavior of peats. Geotechnical Testing Journal, 1980, 3, p. 105-114.
10. Gofar N., Sutejo Y. Long-term compression behavior of fibrous peat. Malaysian J. of Civil Eng., 2007, 19, р. 104-116.
11. Huat B.B.K., Prasad A., Asadi A., Kazemian S. Geotechnics of organic soils and peat. - CRC Press. Taylor&Francis Group, 2014, 263 p.
12. Kogure K., Yamaguchi H., Shogaki T. Physical and pore properties of fibrous peat deposit. Proceedings of the 11th Southeast Asian Geotechnical Conference, Singapore, 1993, p.135-139.
13. Malinowska E.E. Tertiary compression of Polish peat. Scientific Review - Engi-neering and environmental sciences, 2016, 25(4), p. 507-517.
14. O’Kelly B.C., Pichan S.P. Effects of decomposition on the compressibility of fi-brous peat - A review. Geomechanics and Geoengineering, 2013, V.8 (4), p. 286-296.
15. Tyurin D.A., Nevzorov A.L. Numerical simulation of long-term peat settlement under the sand embankment. 1st International conference on the material point method. Pro-cedia engineering, 2017, V.175, p. 51-56.
16. Wong L.S., Hashim R., Ali F.H. A review on hydraulic conductivity and com-pressibility of peat. Journal of Applied Sciences, 2009, 9 (18), p. 3207-3218.
17. Yilmaz E., Saglamer A. Secondary and tertiary compression behavior of samsun soft blue clay. Proceeding of the 15th International Conference on soil mechanics and ge-otechnical engineering, Istambul, Turkey, 2001, V.1-3, p. 329-332.
18. Zhang L., O’Kelly, B.C.Effect of salt grain additions on fibrous peat consolidation. Proceeding of the institution of civil engineers, 2015, 168, p.14-21.
