Россия
Россия
Россия
Россия
Россия
Россия
На промышленных предприятиях при проведении производственных процессов потребляются значительное количество энергетических ресурсов, в том числе и электроэнергии. Поэтому снижение расхода электрической энергии при производстве продукции является важной и актуальной задачей, решение которой обеспечивает снижение себестоимости выпускаемой продукции и в конечном итоге повышение конкурентной способности предприятия на различных рынках. Решение данной задачи осложняется тем, что уровень потребления электроэнергии на том или предприятии зависит от многих факторов, одна часть которых выражается в виде количественных данных, а другая – в виде качественных. Кроме этого, как первая, так и вторая группа данных в большинстве случаев имеет неопределённость и неполноту используемой информации. Эти особенности создают значительные трудности для получения обоснованных и объективных оценок эффективности использования электрической энергии на промышленных предприятиях. Преодоление таких трудностей во многом возможно с применением математического аппарата нечёткой логики. Полученные результаты позволяют получать объективные и обоснованные оценки влияния различных факторов, выражаемых как в количественной, так и в качественной форме на эффективность потребления электрической энергии в производственных процессах промышленных предприятий. Применение таких оценок позволит разрабатывать и применять действенные мероприятия по снижению потребления электроэнергии. Внедрение результатов работы способствует повышению эффективности использования электроэнергии на промышленных предприятиях, что обеспечивает повышение его конкурентной способности.
электрическая энергия, компьютерное моделирование, нечёткая логика, потребление электроэнергии, энергетическая эффективность, оценка эффективности, базы знаний, функции принадлежности
Актуальность работы
На промышленных предприятиях при проведении производственных процессов потребляются значительное количество энергетических ресурсов, в том числе и электроэнергии. Поэтому снижение расхода электрической энергии при производстве продукции является важной и актуальной задачей, решение которой обеспечивает снижение себестоимости выпускаемой продукции и в конечном итоге повышение конкурентной способности предприятия на различных рынках.
Решение данной задачи осложняется тем, что уровень потребления электроэнергии на том или предприятии зависит от многих факторов, одна часть которых выражается в виде количественных данных, а другая – в виде качественных. Кроме этого, как первая, так и вторая группа данных в большинстве случаев имеет неопределённость и неполноту используемой информации. Эти особенности создают значительные трудности для получения обоснованных и объективных оценок эффективности использования электрической энергии на промышленных предприятиях. Преодоление таких трудностей во многом возможно с применением математического аппарата нечёткой логики.
Цель работы является разработка нечёткой математической модели и на её основе системы нечёткого логического вывода, обеспечивающей нахождение значений оценки эффективности использования электрической энергии на промышленных предприятиях.
Формулировка задачи
Изучить факторы, влияющие на эффективность потребления электрической энергии на промышленных предприятиях, разработать нечёткую математическую модель и систему нечёткого логического вывода для получения обоснованной оценки эффективности потребления электроэнергии производственным и энергетическим оборудованием промышленного предприятия.
Введение
Энергетическое хозяйство промышленного предприятия представляет собой сложную для моделирования и исследования производственную подсистему, являющуюся составной частью общей системы промышленного предприятия. Для нее характерно наличие большой размерности, сложность существующих прямых и обратных связей между ее основными элементами, нерегулярным распределением потребления топливно-энергетических ресурсов во времени, присутствием в ее составе разнородных составляющих [1].
Получение обоснованной оценки эффективности работы любой производственной системы (как всего промышленного предприятия, так составляющих ее подсистем) является задачей выработки и принятия управленческих решений, решаемой методами системного анализа. В итоге решения такой задачи должны быть получены интегральные или обобщённые показатели (или показатель) качества функционирования всех производственных элементов, характеризующие системную эффективность деятельности рассматриваемой производственной системы [2, 3]. Такая обобщенная оценка вырабатывается с применением самых разных критериев и факторов, учитывающих разнообразную информацию, имеющую как объективный, так и субъективный характер.
Форма и структура создаваемой для решения задачи определения эффективности потребления энергоресурсов на промышленном предприятии математической модели определяются существующими в рассматриваемой системе процессами, наличием внутренних и внешних факторов, характером количественных и качественных взаимосвязей между этими факторами. Также модель должна учитывать степень влияния на получаемый результат действующих в изучаемой системе процессов и какие факторы должны учитываться в первую очередь при рассмотрении системы, принимая во внимание при этом конкретную поставленную задачу, применяемые средства и методы проводимого исследования.
Основные сложности при разработке математических моделей для изучения процессов энергопотребления в различных системах, в том числе и на промышленных предприятиях, состоят прежде всего в больших объемах используемых для этой цели данных [4 - 11]. Эта задача еще более усложняется в том случае, когда используемые исходные данные обладают, пусть и не в полной мере, неопределенностью и неполнотой, особенно когда формирование итоговой оценки или же результат решения задачи во многом зависят от такой информации.
Появление неопределенности в исходной информации при решении задач управления и анализа для больших производственных систем, включая и энергетические хозяйствах промышленных предприятий, от нормального функционирования которых во многом зависят итоговые показатели работы предприятий, происходит по многим причинам, среди которых следует выделить:
– наличие неполных или даже отсутствие достоверных знаний, выражаемых в количественной форме;
– серьезные ограничения, возникающие при возможном проведении исследований протекающих в системе процессов, что является актуальным аспектом, когда существуют различные формы собственности на предприятиях;
– необходимость применения многокритериальной оценки, когда принимаются во внимание различные показатели функционирования изучаемой системы, а также разнородность (количественная и качественная форма) в используемых для этой цели данных.
Необходимость учета многих факторов при исследовании процессов потребления электроэнергии показана во многих исследованиях. Так, в работе [1] предложено применение динамической оценки эффективности энергопотребления как определенное соотношение темпов роста энергетических и экономических критериев развития предприятия.
Эта оценка должна формироваться с учетом следующих показателей:
- темпы роста прибыли от реализации товарной продукции;
- темпы роста реализованной товарной продукции (Д);
- темпы роста использования вторичных энергоресурсов;
- темпы роста электропотребления;
- темпы роста затрат на энергоснабжение;
- темпы роста объемов энергоресурсов, потребляемых предприятием;
- темпы роста валовых выбросов вредных веществ от сжигания топлива в атмосферу региона.
Такая динамическая оценка все же не дает объективной картины эффективности использования электроэнергии на промышленном предприятии, так как применяемая исходная информация рассматривает темпы роста относительно некоторых предыдущих значений, которые могут быть достаточно низкими и в итоге даже достаточно быстрые темпы роста используемых факторов все же не обеспечивают высокой энергетической эффективности предприятия. Кроме этого, перечисленные выше исходные факторы не обеспечивают в полной мере достоверность получаемой оценки, например, не учитывается степень загрузки оборудования и другие важные показатели.
Поэтому для получения обоснованной оценки эффективности потребления электроэнергии на промышленных предприятиях следует использовать довольно большое количество исходных показателей, выражаемых как в количественной или числовой форме, так и в качественной форме [12, 13].
Исходя из приведенных выше материалов, делаем вывод, что для построения математической модели, предназначенной для получения обоснованной оценки эффективности использования предприятием энергетических ресурсов, в первую очередь электроэнергии, следует использовать математический аппарат теории нечёткой множеств или нечёткой логики. Исходя из такого подхода, математическая модель разрабатывается с учетом существующих в рассматриваемой системе причинно-следственных связей между входными и выходными показателями ее функционирования.
Такая нечёткая математическая модель будет намного ближе по своей структуре и работе к мыслительным процессам человека, чем модель, построенная на традиционном подходе и состоящая из линейных и нелинейных алгебраических и дифференциальных уравнений. Ее применение позволит учитывать и обрабатывать неопределенность, неполноту исходных данных, а также использовать опыт экспертов в области энергетики. На основе таких моделей создаются системы нечеткого логического вывода (СНЛВ), реализующие процессы получения нечетких оценок о текущем состоянии изучаемой системы [14 -16].
Методология
Система нечёткого вывода предназначена для реализации процессов нахождения нечетких заключений о текущем состоянии изучаемой рассматриваемой системы (в нашем случае процессов потребления электрической энергии) на базе нечетких заключений, использующих как количественные, так и качественные данные по рассматриваемому объекту. Создание и последующее практическое применение СНЛВ выполняется в несколько этапов, каждый из которых осуществляется на основе применения известных методов нечеткой логики, приведенных в различных источниках. например [16-20]. Сам процесс логического вывода включает в себя следующие этапы, показанные на рис. 1:
- введение нечеткости (фаззификация на основе функций принадлежности);
- нечеткий вывод (на основе базы знаний или базы правил);
- композиция и приведение к четкости (дефаззификация с применением функций принадлежности).
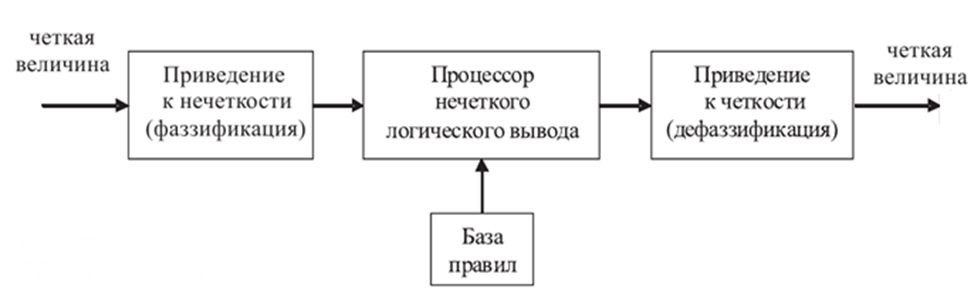
Рис. 1. Схема нечёткого логического вывода
Входной информацией или входными переменными для разрабатываемой СНЛВ являются факторы, от которых зависит эффективность потребления электрической энергии на рассматриваемом предприятии. Значение выходной переменной представляет собой оценку энергоэффективности изучаемого предприятия. Для построения подобной СНЛВ используем такую разновидность систем нечеткого логического вывода как MISO-системы. Данные системы имеют многочисленные, (в общем случае n) входные переменные (по числу принятых к рассмотрению факторов, влияющих на энергоэффективность) и только одну выходную переменную. Системы типа MISO реализуют отображение множества выходных переменных на область значений выходной в следующем виде:
y = f (x1, x2, x3, .... xn), (1)
где y – выходная переменная, представляет собой оценку эффективности использования энергетических ресурсов; x1, x2, x3, .... xn – входные переменные, соответствующие рассматриваемым исходным данным или факторам.
Используемые для работы СНЛВ исходные данные представляются вектором X, определенным в свою очередь на декартовом произведении областей задания входных переменных, записываемом в следующем виде: X1×X2×X3×....× Xn. Функция f производит отображение вектора входных переменных X на область значений выходной величины Y.
Факторы, влияющие на эффективность потребления электроэнергии на предприятии, представляем как некоторое свойство изучаемой системы, рассматриваемой в создаваемой нечёткой математической модели. Данные факторы в модели оценивается качественным образом, например: «уровень физического и морального износа производственного оборудования». Поэтому, для каждого такого фактора должна быть установлена в соответствие своя лингвистическая переменная, характеризуемая терм-множеством Ti ={T1i, T2i,…Tmi}. Термы данного множества составляют нечеткие значения всех возможных состояний рассматриваемого фактора, например, «низкий», «ниже среднего», «средний», «выше среднего», «высокий»; а также синтаксические и семантические правила.
Покажем разработку такой СНЛВ на примере одного из предприятий Курской области - ООО «Биаксплен». Для построения этой системы применяем исходные данные, учитывающие влияние на эффективность потребления энергетических ресурсов различных факторов, представленных ниже. Исходная информация представляется сочетанием использования численных значений и соответствующих этим данным экспертным оценкам, так и чисто экспертным оценкам. Для разработки СНЛВ применяем модель Мамдани [18-20].
Проведем классификацию используемых факторов, влияющих на эффективность использования электрической энергии на рассматриваемом промышленном предприятии.
К группе экономических факторов относятся:
- материальное стимулирование персонала, осуществляющего разработку и внедрение энергосберегающих мероприятий;
- уровень цен и тарифов на топливно-энергетические ресурсы;
- доходность промышленного производства.
В группу производственных факторов входят:
- загрузка производственных мощностей;
- уровень физического и морального износа основных производственных фондов;
- материалоемкость производства или выход готовой продукции из исходного сырья);
- технологическая производительность (выход готовой продукции за один час);
- внедрение прогрессивных технологических процессов;
- значение количества потерь сырья.
К организационным факторам относятся:
- планирование, как производственных процессов, так и процессов энергосбережения;
- учет и контроль за потреблением ТЭР.
В группу социальных факторов входят:
- численность персонала по отношению к аналогичным производствам;
- квалификация и образование персонала.
Согласно приведенного перечня факторов всего в создаваемой СНЛВ должно быть задействовано 12 входных параметров, или система должна иметь 12 входов. Известно, что моделирование многомерных зависимостей «входы-выход» лучше всего выполнять на базе иерархических систем нечеткого вывода. Данные системы характерны тем, что выход одной базы знаний, учитывающей взаимные связи между факторами одной и той же группы, соединяется с входом другой базы знаний, находящейся на более высоком уровне иерархической структуры.
Кроме этого, применение иерархических систем нечеткого вывода позволит избежать составления большого числа правил в базе знаний. Число правил в базе знаний r, задающих простые условия, определяется по следующей формуле:
r = zw, (2)
где z – число нечетких правил в базе знаний; w – число входов модели или число входных переменных.
Из этой формулы следует, что число правил в базе знаний увеличивается по экспоненте с увеличением числа применяемых входных переменных. Поэтому применение в СНЛВ иерархической структуры позволяет применять сравнительно простые базы знаний.
Такой подход к разработке СНЛВ позволяет во многом избежать трудностей, связанных с большим количеством используемых данных для изучения производственных систем. В противном случае, при большом количестве входных параметров и одном выходном эксперту или группе экспертов становится сложно представить нечеткими правилами существующие взаимосвязи между исходной информацией и итоговой оценкой в данной системе. Это связано с тем фактом, что в памяти человека не может одновременно находиться и обрабатываться значительное количество информации.
Опыт разработчиков систем нечеткого вывода показывает, что оптимальное число входов для базы знаний не должно превышать пяти. Таким образом, при большем количестве входных переменных следует вводить иерархическое разделение. Выполнение такого построения систем нечеткого вывода не составляет трудностей для эксперта, так как процесс обработки информации человеком происходит по иерархическому принципу.
Еще одним преимуществом иерархических баз знаний – компактность. Небольшим количеством нечетких правил в иерархических базах знаний можно адекватно описать многомерные зависимости «вход – выход».
Исходя из этого, СНЛВ для оценки эффективности процессов потребления электроэнергии на промышленных предприятиях будем разрабатывать в виде иерархической системы. Эта система может быть представлена в виде иерархического дерева (или системы из нескольких уровней) – рис. 2.

Рис. 2. Иерархическая система нечёткого вывода
Существующие связи в иерархической СНЛВ легко представляется в виде некоторого дерева, включающего в себя корень или же главную вершину дерева, промежуточные или терминальные вершины, нетерминальные вершины и ветви дерева, образующие связи между вершинами. Более подробно элементы данного дерева можно охарактеризовать так:
- корень дерева представляет собой значение эффективности потребления электроэнергии на рассматриваемом промышленном предприятии или выходную переменную Z;
- терминальные или промежуточные вершины это частные, влияющие на эффективность потребления электрической энергии, факторы (X1,.., Xk);
- нетерминальные вершины (двойные окружности) ‑ свертки влияющих факторов или подсистемы промежуточного вывода;
- дуги графа (ветви дерева), выходящие из нетерминальных вершин ‑ укрупненные влияющие факторы (Y1 - Yn).
В итоге, нечёткая модель определения эффективности потребления электрической энергии промышленным предприятием будет представлять функциональное отображение вектора входных переменных X на область значений выходной переменной Z (от нуля до 100) следующего вида:
X = (X1,.., X13 ) → Z[0,100] . (3)
В качестве значений выходной переменной используются следующие качественные оценки, характеризующие общее состояние эффективности потребления электроэнергии на промышленном предприятии:
- от 0 до 20 – уровень эффективности потребления электроэнергии на промышленном предприятии «очень низкий», необходим незамедлительное проведение энергетических обследований и внедрение энергосберегающих мероприятий в значительном объеме;
- от 20 до 40 – уровень состояния эффективности потребления электроэнергии на промышленном предприятии «низкий», требуется выявление наиболее энергорасточительных производственных процессов и внедрение энергосберегающих мероприятий;
- от 40 до 60 – уровень состояния эффективности потребления электроэнергии «средний», необходимо внедрение энергосберегающих мероприятий;
- от 60 до 80 – уровень «выше среднего», рекомендована дополнительная обработка исходной информации для уточнения состояния энергетического хозяйства предприятия и принятия различных мер по улучшению его состояния при необходимости;
- от 80 до 100 – уровень «высокий», энергетическое хозяйство предприятия находится в нормальном состоянии, не требующем осуществления в настоящее время каких-либо дополнительных действий.
Для построения функций принадлежности применялся метод, по которому эксперт оценивает превосходство одного рассматриваемого элемента над другим по отношению этих элементов к рассматриваемому свойству применяемого нечёткого множества. Эти сравнения пар элементов можно выразить в виде матрицы A:
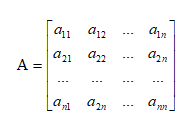 , (4)
, (4)
где aij – значение преимущества по мнению эксперта элемента vi над vj, определяемое по шкале в девять баллов, согласно, метода анализа иерархий, предложенного Саати.
Далее степени принадлежности для элементов нечеткого множества принимаются равными соответствующим координатам собственного вектора W матрицы парных сравнений A:
W = (w1, w2, ….. , wn). (5)
Сам же собственный вектор можно найти двумя способами. Первый способ состоит в решении следующей системы уравнений:
A∙W = λmax∙ W, (6)
w1 + w2 + ….+ wn =1,
где λmax - максимальное по величине собственное значение матрицы парных сравнений A.
По второму способу нахождение собственного вектора осуществляется с использованием средств современных программ научно-технических расчетов, например, бесплатно распространяемой компьютерной системы SciLab. В этой системе имеется встроенная функция вида spec() для получения собственного вектора или вектора собственных значений, используя которую находим искомый вектор:
W = spec(A). (7)
Учитывая тот факт, для каждой из входных переменных имеется относительно небольшой объем имеющейся информации, были применены простые функции принадлежности, состоящие из прямолинейных участков или же многоугольные функции. Для функций такого вида нетрудно обеспечить выполнение условия, согласно которого сумма степеней принадлежности каждого из элементов нечеткого множества должна быть равной 1.
Для работы с крайними термами были использованы трапециевидные функции принадлежности, так как желательно, чтобы значения степеней принадлежности этих термов вблизи границ интервала были как можно ближе к единице. Для средних термов использованы треугольные функции принадлежности,
Для формирования базы правил используются данные, поступающие от экспертов, а также значения, полученные в результате обследований различного энергетического и технологического оборудования.
Первоначально каждый пример из выборки получает в соответствие отдельное правило. Множество таких примеров обучающей выборки задается с помощью формулы:
(x1(k), x2(k), x3(k), x4(k), x5(k) ... xn(k), y ), k =1, …, K, (8)
где x1(k), x2(k), x3(k), x4(k), x5(k) ... xn(k) – значения n входных переменных; y – значение выходной переменной y в k-м примере; K – общее количество примеров в обучающей выборке.
Базы правил вывода для разрабатываемой системы СНЛВ создавались в два этапа. На первом этапе разрабатываются базы правил для подсистем промежуточного вывода. Для примера показана одна такая база в ниже приведенной табл.1. На втором – база для окончательного вывода, приведенная в табл.2.
Таблица 1.
База правил для подсистема экономических факторов
|
X1 |
X2 |
X3 |
Y1 |
|
Высокий |
Низкая |
Низкое |
Низкий |
|
Высокий |
Низкая |
Высокое |
Высокий |
|
Высокий |
Высокая |
Высокое |
Высокий |
|
Высокий |
Высокая |
Низкое |
Высокий |
|
Низкий |
Низкая |
Низкое |
Низкий |
|
Низкий |
Низкая |
Высокое |
Низкий |
|
Низкий |
Высокая |
Низкое |
Низкий |
|
Низкий |
Высокий |
Высокое |
Высокий |
Таблица 2.
База правил окончательного вывода
|
Y1 |
Y2 |
Y3 |
Y4 |
Z |
|
Высокий |
Низкий |
Высокий |
Низкий |
Cредний |
|
Высокий |
Высокий |
Низкий |
Высокий |
Высокий |
|
Высокий |
Низкий |
Высокий |
Низкий |
Средний |
|
Низкий |
Высокий |
Низкий |
Высокий |
Средний |
|
Низкий |
Низкий |
Высокий |
Низкий |
Низкий |
|
Низкий |
Высокий |
Низкий |
Высокий |
Средний |
Результаты и их обсуждение
Непосредственное создание рассматриваемой в данной статье СНЛВ осуществлялось в компьютерной системе научно-технических расчетов MatLab, с применением пакета Fuzzy Logic Toolbox. В состав данного пакета входит редактор систем нечёткого вывода FIS, используемый для создания или редактирования систем нечёткого вывода в графическом режиме. Графический интерфейс данного редактора обладает удобством и гибкостью, которые являются необходимыми для интерактивной работы с отдельными компонентами системы нечеткого вывода, в том числе создание функций принадлежности и базы правил. Для примера на рис. 3 показано задание функций принадлежности для входной переменной X2, характеризующей уровень цен на электроэнергию, пределы изменений которой были приняты от 3000 до 4200 руб/тыс.кВт∙час, при действующем на момент разработки СНЛВ значении 3906,93 руб/тыс.кВт∙час.
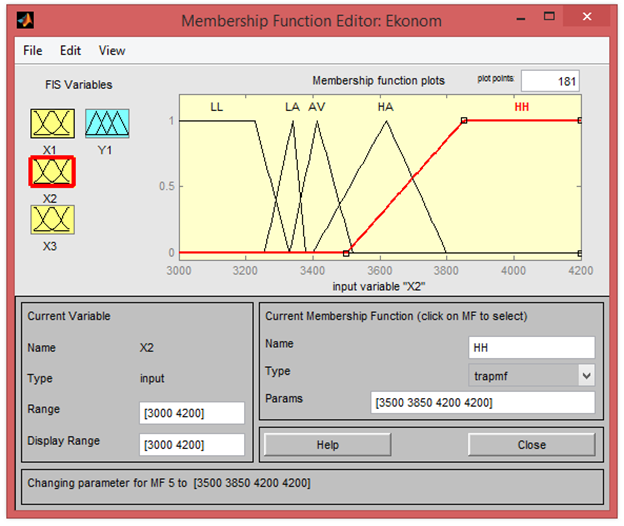
Рис. 3 - Создание функций принадлежности для входной переменной X2
Для лингвистической оценки этой переменной используются два терма с трапециевидными функциями принадлежности (HH – высокий, LL - низкий) и три терма с треугольными функциями принадлежности (LA – ниже среднего, AV - средний, HA – выше среднего).
После создания СНЛВ, используя значения входных переменных, действующие в данный момент времени на предприятии (не приведенные в статье из-за ограниченного объема), было получено выходное значение Z = 65. Оно соответствует уровню эффективности «Выше среднего», при таком уровне целесообразна провести дополнительную обработку исходной информации для уточнения состояния энергетического хозяйства предприятия.
Выводы и рекомендации
В статье рассмотрено и обосновано применение математического аппарата нечёткой логики для моделирования процессов потребления и преобразования электроэнергии на промышленном предприятии и получения обоснованной оценки эффективности данных процессов. Для создания СНЛВ, обеспечивающей получение оценки эффективности процессов потребления и преобразования электроэнергии на промышленном предприятии, рассмотрены основные факторы различной природы, непосредственно влияющие на протекание процессов в энергетическом хозяйстве рассматриваемого предприятия.
Эта система реализована с применением иерархических баз знаний, что обеспечивает эффективность применения экспертных знаний из-за небольшого объема информации, с которым работает каждый эксперт, участвующий в подготовке данных для разрабатываемой системы нечеткого логического вывода. С применением данной системы была получена оценка эффективности процессов потребления электроэнергии на рассматриваемом предприятии «Выше среднего». Данная оценка обосновывается применением информации, выраженной как количественными значениями, так и чисто качественными.
Публикация выполнена в рамках государственного задания № 0851-2020-0034.
1. Кокшаров В.А. Совершенствование методического инструментария оценки энергоэффективности промышленного предприятия // Вестник Пермского университета. Сер. «Экономика» = PermUniversity Herald. Economy. 2016. № 3(30). С. 168-181. doi:https://doi.org/10.17072/1994-9960-2016-3-168-181.
2. Ермолаев К.А. Влияние процессов энергосбережения и повышения энергоэффективности на инновационное развитие национальных экономик // Экономический анализ: теория и практика. 2017. Т. 16. Вып. 1. С. 82-92. URL: https://doi.org/10.24891/ea.16.1.82
3. Клочков В.В. Анализ влияния технологических сдвигов в энергетике на устойчивость российской экономики // Национальные интересы: приоритеты и безопасность. 2017. Т. 13. Вып. 4. С. 684-698. URL: https://doi.org/10.24891/ni.13.4.684
4. Лебедев В.А. Эксергетический метод оценки энергоэффективности оборудования систем энергообеспечения предприятий минерально-сырьевого комплекса/ В.А. Лебедев// Записки Горного института. - 2016. - Т.219. - С.435-443. DOIhttps://doi.org/10.18454/PMI.2016.3.435.
5. Перелыгин В.В., Склярова Н.А., Мирошниченко Ю.В., и др. Обеспечение энергетической эффективности на предприятиях фармацевтической промышленности в парадигме снижения техногенной нагрузки на окружающую среду // Формулы Фармации. - 2020. - Т. 2. - №4. - C. 104-117. doi:https://doi.org/10.17816/phf50668
6. Мельник А.Н., Ермолаев К.А. Концептуальные основы управления энергосбережением и повышением энергоэффективности на промышленном предприятии в условиях его инновационного развития // Экономический анализ: теория и практика. - 2019. - Т. 18, No 1. - С. 22 - 39. https://doi.org/10.24891/ ea.18.1.22
7. Кокшаров В.А. Методический подход оценки приоритетов энергетической политики промышленного предприятия // Статистика и Экономика. 2015. № 2. С. 72-77. URL: https://doi.org/10.21686/2500-3925-2015-2-72-77
8. Макаркин Н.П., Горина А.П., Алферина О.Н., Корнеева Н.В., Потапова Л.Н. Эффективность использования ресурсного потенциала предприятия: методика оценки// Фундаментальные исследования. - 2019. - № 11. - С. 89-94; DOIhttps://doi.org/10.17513/fr.42592
9. Криворотов В. В., Калина А. В., Савельева А. И. Оценка энергоэффективности компаний медной промышленности: теория и практика // Известия Уральского государственного экономического университета. 2018. Т. 19, No 4. С. 107-116. DOI:https://doi.org/10.29141/2073 1019 2018 19 5 8
10. Кокшаров В.А. Систематизация факторов энергоэффективности промышленного предприятия // Вестник Пермского университета. Сер. «Экономика» = Perm University Herald. Economy. 2016. No 1(28). С. 147-156.
11. Перелыгин В.В., Склярова Н.А., Мирошниченко Ю.В., и др. Обеспечение энергетической эффективности на предприятиях фармацевтической промышленности в парадигме снижения техногенной нагрузки на окружающую среду // Формулы Фармации. - 2020. - Т. 2. - №4. - C. 104-117. doi:https://doi.org/10.17816/phf50668
12. Шаталова, О.М. Об использовании нечетких вычислений в решении проблемы неопределенности при оценке эффективности технологических инноваций на предприятии // Вестник ЮУрГУ. Серия «Экономика и менеджмент». - 2018. - Т. 12, № 3. - С. 83-91. DOI:https://doi.org/10.14529/em180309
13. Шаталова, О.М. Основные положения методики информационного обеспечения в оценке эффективности технологических инноваций методами нечеткого моделирования // Вестник ЮУрГУ. Серия «Экономика и менеджмент». - 2018. - Т. 12, № 4. - С. 102-112. DOI:https://doi.org/10.14529/em180413
14. Леденева Т.М. Особенности реализации механизма нечеткого логического вывода в нечетких системах / Т. М. Леденева, А. Д. Решетников // Международный научно-исследовательский журнал. - 2021. - № 6 (108) Часть 1. - С. 107-117. - URL: https://research-journal.org/technical/ osobennosti-realizacii-mexanizma-nechetkogo-logicheskogo-vyvoda-v-nechetkix-sistemax/ (дата обращения: 02.10.2021.). doi:https://doi.org/10.23670/IRJ.2021.108.6.018
15. Ledeneva, T. Analysis of additive generators of fuzzy operations represented by rational functions // Journal of Physics: Conf. Series. - 2018. - №973. doi https://doi.org/10.1088/1742-6596/973/1/012037.
16. Голосовский М.С., Богомолов А.В., Теребов Д.С., Евтушенко Е.В. Алгоритм настройки системы нечёткого логического вывода типа Мамдани // Вестник ЮУрГУ. Серия: Математика. Механика. Физика. 2018. №3. URL: https://cyberleninka.ru/article/n/algoritm-nastroyki-sistemy-nechyotkogo-logicheskogo-vyvoda-tipa-mamdani (дата обращения: 02.10.2021). doihttps://doi.org/10.14529/mmph180303
17. Шилова С.В., Бурмистрова О.Н. Композиция Мамдани в моделях нечеткого анализа как нечеткий аналог подстановок зависимостей// Современные наукоемкие технологии. - 2021. - № 10. - С. 102-107; URL: https://top-technologies.ru/ru/article/view?id=38861 (дата обращения: 02.10.2021). DOIhttps://doi.org/10.17513/snt.38861
18. Segismundo S. Izquierdo, Luis R. Izquierdo Mamdani Fuzzy Systems for Modelling and Simulation: A Critical Assessment. Journal of Artificial Societies and Social Simulation, 21(3) 2, 2018 Url: http://jasss.soc.surrey.ac.uk//21/3/2.html. Doi:https://doi.org/10.18564/jasss.3444.
19. W.B. Zulfikar, Jumadi, P.K.Prasetyo, M.A.Ramdhani. Implementation of Mamdani Fuzzy Method in EmployeePromotion System IOP Conf. Series: Materials Science and Engineering 288 (2017) 012147 doihttps://doi.org/10.1088/1757-899X/288/1/012147
20. A.A.I. Dwi Fibriayora, G.K. Gandhiadi, N.K.T. Tastrawati, Eka N. Kencana. Application of Mamdani fuzzy method to determine round bread production at pt Vanessa bakery. E-Jurnal Matematika Vol. 8(3), Agustus 2019, pp.204-210. DOI: https://doi.org/10.24843/MTK.2019.v08.i03.p254


















