с 01.01.2015 по настоящее время
Россия
Ростов на дону, Ростовская область, Россия
с 01.09.2014 по настоящее время
Казанский (Приволжский) федеральный университет (Институт дизайна и пространственных искусств, Главный научный сотрудник)
Батайск, Ростовская область, Россия
В статье представлено численное и аналитическое решение задачи оптимизации сжатых стержней по критерию максимума критической нагрузки при возможной потере устойчивости в двух плоскостях. Рассматриваются деревянные стойки прямоугольного поперечного сечения, высота которого меняется по линейному закону, а ширина постоянна. Расчет выполняется в упругой постановке. Вводится ограничение на постоянство массы стержня. В качестве варьируемых параметров выступают отношение минимальной высоты сечения к максимальной, а также отношение ширины сечения к максимальной высоте. Численный поиск оптимального решения выполняется в среде MATLAB при помощи метода последовательного квадратичного программирования. Установлено, что применение стержней с линейно меняющейся по длине высотой поперечного сечения эффективно только в том случае, когда хотя бы в одной из плоскостей стержень закреплен по схеме «защемление – свободный конец». Установлено, что прирост критической нагрузки при использовании стержней с линейно меняющейся высотой сечения может составить до 22%.
стержень, дерево, устойчивость, оптимизация, последовательное квадратичное программирование.
Введение
Древесина на протяжении многих веков является одним из основных конструкционных материалов в строительстве, что обусловлено ее высокими физико-механическими и техническими качествами. На современном этапе развития строительной отрасли в области проектирования и возведения зданий и сооружений с использованием конструкций из дерева имеет место значительный прогресс благодаря применению клееных деревянных конструкций [1-3].
Для совершенствования проектных решений и снижения материалоемкости строительства требуется разработка и развитие научно-обоснованных методов расчета и оптимизации строительных конструкций. Во многих конструкциях используются элементы с постоянной по длине геометрией поперечного сечения, однако из соображений уменьшения расхода материала в некоторых случаях целесообразно применять элементы переменной жесткости [4-6].
Постановка задачи о наивыгоднейшем очертании колонны принадлежит Ж.Л. Лагранжу. Подробный обзор аналитических решений задачи Лагранжа представлен в работах А.П. Сейраняна [7-8]. Особенностью аналитических решений задачи оптимизации сжатой колонны является наличие точек с нулевой площадью, где будут возникать бесконечные напряжения. Таким образом, для создания реальных конструкций эти решения неприменимы.
Решение с учетом ограничения на минимальную площадь поперечного сечения может быть выполнено с использованием численных методов. Численные решения задач оптимизации сжатых стержней приведены в работах [9-13]. В указанных публикациях найденная оптимальная форма стержня описывается нелинейной функцией, что затрудняет практическую реализацию таких решений, особенно в случае использования дерева в качестве конструкционного материала. Представляет интерес решение задач оптимизации стержней с линейно меняющейся высотой поперечного сечения и определение области их эффективного использования.
Методы
Рассматривается упругая деревянная стойка прямоугольного поперечного сечения, ширина которой постоянна и равна b, а высота меняется от h0 до βh0 по линейному закону (рис. 1). Стойка сжимается силой F. В качестве варьируемых параметров примем высоту h0, отношение β, а также параметр α=b/h0. Стойка может иметь различные закрепления в плоскостях xz и xy, коэффициенты приведения длины в этих плоскостях равны μxz и μyz соответственно. Требуется найти такие значения параметров α и β, чтобы критическая сила достигла максимума при постоянной массе стержня.
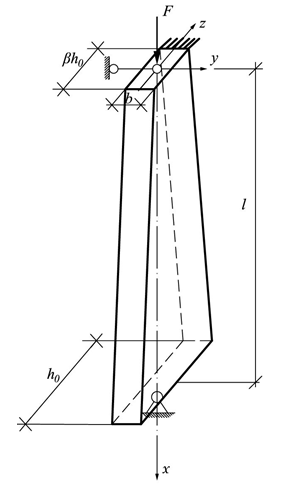
Рис. 1. Расчетная схема
Объем стержня можно вычислить по формуле:
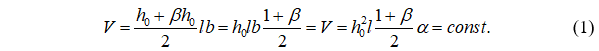
Выразим из (1) h0:
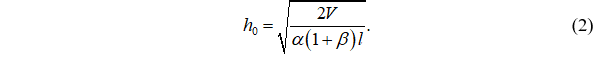
Для стержня постоянного сечения из упругого материала критическая сила определяется по известной формуле Эйлера:
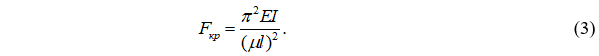
В действующих нормах проектирования деревянных конструкций для стержней с линейно меняющейся высотой поперечного сечения переменная жесткость учитывается коэффицентом kжN, который зависит от способа закрепления и параметра β. Уточнение нормативных формул коэффициента kжN нами было выполнено ранее. Расчетные формулы для коэффициента kжN представлены в таблице 1.
Табл. 1. Расчетные формулы коэффициента kжN
| закрепление | μ | плоскость xz | плоскость xy |
| шарнир-шарнир | 1 | 0.5116β2+0,5004β-0,0103 | -0,1305β2+0,7193β+0,4079 |
| шарнир-защемление | 0,7 | 0,515β2+0,5054β-0,0157 | -0,1731β2+0,793β+0,3783 |
| защемление-защемление | 0,5 | 0,5158β2+0,5037β-0,0172 | -0,2186β2+0,8624β+0,3499 |
| защемление-свободный край | 2 | -0,1158β2+1,0848β+0,025 | -0,1236β2+0,5089β+0,612 |
Критическая сила при потере устойчивости в плоскости xz может быть вычислена как:
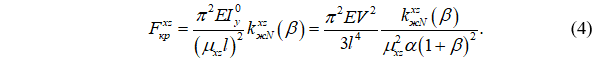
При потере устойчивости в плоскости xy формула критической силы принимает вид:
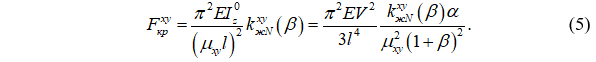
Целевую функцию представим в виде:
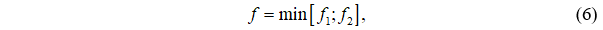
где 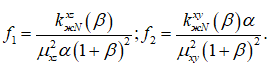
Требуется найти такие α и β, чтобы целевая функция принимала максимальное значение.
Решение задачи нелинейной оптимизации выполнялось в среде MATLAB с использованием пакета Optimization Toolbox для всех возможных сочетаний μxy = [0,5; 0,7; 1; 2] и μxz = [0,5; 0,7; 1; 2]. В качестве оптимизационного метода использовался алгоритм последовательного квадратичного программирования (SQP) [14-16]. Для β принимался диапазон возможных значений от 0,1 до 1, а для α — от 0,1 до 10.
Результаты и обсуждение
Полученные в результате оптимальные значения параметров α и β сведены в табл. 2.
Табл. 2. Оптимальные значения параметров α и β при различных закреплениях в двух плоскостях
|
μxz μxy |
0,5
|
0,7
|
1
|
2
|
| 0,5 | α=0,9817 β=0,9593 |
α=0,7021 β=0,9593 |
α=0,4877 β=0,9479 |
α=0,2162 β=0,5036 |
| 0,7 | α=1,3957 β=0,9905 |
α=0,9924 β=0,9801 |
α=0,6865 β=0,961 |
α=0,2998 β=0,4911 |
| 1 | α=2 β=1 |
α=1,4309 β=0,9955 |
α=0,991 β=0,9784 |
α=0,4235 β=0,4742 |
| 2 | α=3,4156 β=0,7719 |
α=2,4346 β=0,7671 |
α=1,6883 β=0,7556 |
α=0,731 β=0,3765 |
В табл. 2 серым выделены варианты, для которых оптимальный параметр β оказался близок к 1. Для этих вариантов использование переменного сечения неэффективно. Вообще говоря, для указанных вариантов βопт = 1, а αопт = μxy/μxz (из условия равноустойчивости в двух плоскостях), в чем можно убедиться, если построить поверхности f(α,β). Одна из таких поверхностей, соответствующая μxz=1 и μxy=0,7, показана на рис. 2. Оптимальная точка, найденная при помощи MATLAB, отмечена красным маркером. Отклонение β от 1 связано с тем, что касательная в отмеченной точке и при β=1 практически горизонтальна.
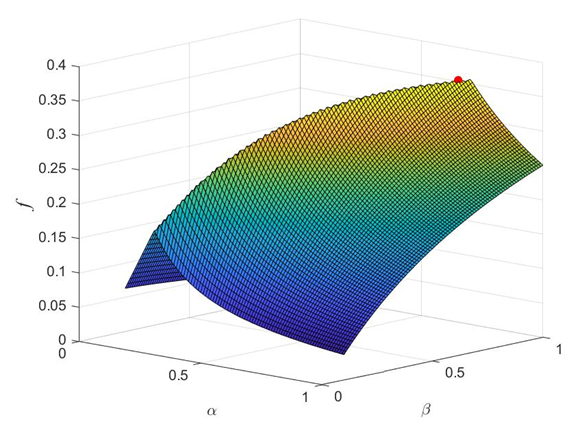
Рис. 2. Поверхность f(α, β) при μxz = 1 и μxy = 0,7
Из таблицы 2 видно, что использование переменного сечения с линейным изменением высоты по длине эффективно, только когда хотя бы в одной из плоскостей стержень закреплен по схеме «защемление-свободный край». На рисунке 3 приведена одна из таких поверхностей f(α,β), соответствующая случаю μxz=2 и μxy=0,5. При любых μxz и μxy поверхности f(α,β) имеют гребень, соответствующий равноустойчивому состоянию, на котором и находится оптимальная точка.
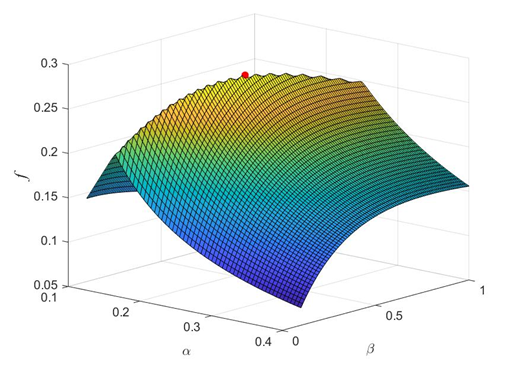
Рис. 3. Поверхность f(α, β) при μxz=2 и μxy=0,5
Положение этого гребня можно найти, если приравнять (4) и (5). В результате получим формулу:
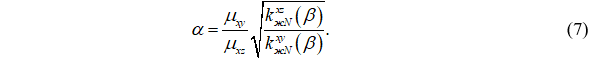
Подстановка (7) в (6) приведет к следующему выражению для целевой функции:
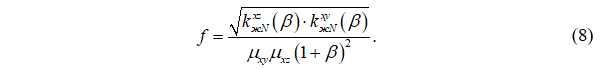
Продифференцируем (8) по β и приравняем к нулю:
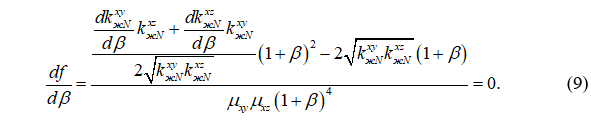
После упрощений задача поиска оптимального β сводится к уравнению:
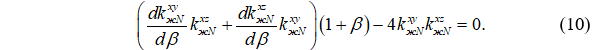
При использовании зависимостей, представленных в действующих нормах расчета деревянных конструкций, для некоторых вариантов закрепления решение уравнения (10) может быть получено аналитически. Так, при μxz=μxy=2:
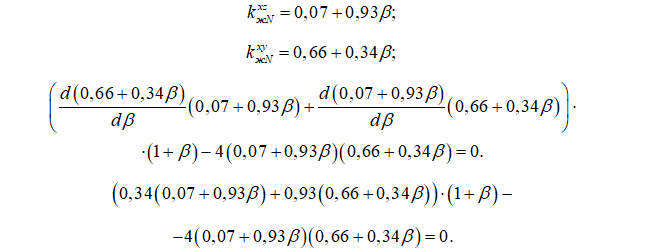
После упрощений имеем квадратное уравнение, которое в диапазоне β∈[0;1] имеет корень β=0,3071. Данное решение несколько отличается от результата, представленного в табл. 2, что объясняется различием нормативных и полученных нами формул коэффициентов kжN. При поиске минимума функции (6) в MATLAB с использованием нормативных формул было получено значение β=0,3072. По сравнению со стержнем постоянного сечения для оптимального стержня критическая нагрузка оказалась выше на 22%. Отметим, что в задаче Лагранжа максимально возможный прирост критической нагрузки составляет 33% [17-20].
Выводы
Аналитически и численно решена задачи оптимизации стержня прямоугольного поперечного сечения, высота которого меняется по линейному закону при возможной потере устойчивости в двух плоскостях. Для различных вариантов закрепления найдены оптимальные значения безразмерных геометрических параметров, обеспечивающие максимум критической нагрузки.
Установлено, что применение стержней с линейно меняющейся высотой целесообразно только в случае, когда по крайней мере в одной плоскости стержень закреплен по схеме «защемление-свободный край».
При использовании стержней переменной жесткости c линейно меняющейся высотой сечения прирост критической нагрузки может составить 22% по сравнению со стержнями постоянной жесткости.
1. Серов, Е. Н. Клееные деревянные конструкции: состояние и проблемы развития / Е. Н. Серов, Б. В. Лабудин //Известия высших учебных заведений. Лесной журнал. - 2013. - №. 2 (332). - С. 137-146.
2. Пашкова, М. Е. Большепролетные деревянные конструкции / М. Е. Пашкова, Е. А. Базарова, В. В. Андриенко //Наука и образование: проблемы, идеи, инновации. - 2018. - №. 5. - С. 18-22.
3. Мещерякова, А. А. Клееные деревянные конструкции и перспективы их использования / А. А. Мещерякова, В. В. Белоконев //Поколение будущего: взгляд молодых ученых. - 2016. - С. 45-48.
4. Немировский, Ю. В. Рациональное проектирование слоистых деревянных конструкций / Ю. В. Немировский, А. И. Болтаев //Проблемы оптимального проектирования сооружений. - 2017. - С. 193-201.
5. Малыхина, В. С. Анализ конструктивных решений деревянных трехшарнирных рам / В. С. Малыхина, А. А. Рязанова //Вестник Белгородского государственного технологического университета им. В. Г. Шухова. - 2018. - №. 6. - С. 33-38.
6. Karamisheva, A. A. Calculation of plane bending stability of beams with variable stiffness / A. A. Karamisheva, S. B. Yazyev, A. A. Avakov //Procedia Engineering. - 2016. - Т. 150. - С. 1872-1877.
7. Сейранян, А. П. Задача Лагранжа о наивыгоднейшем очертании колонны / А.П. Сейранян // Успехи механики. - 2003. - №2. - С. 45 - 96.
8. Seyranian, A. P. The Lagrange problem on an optimal column: old and new results / A. P. Seyranian, O. G. Privalova // Structural and multidisciplinary optimization. - 2003. - Т. 25. - №. 5. - С. 393-410.
9. Чепурненко, А.С. Оптимизация формы поперечного сечения сжатых стержней из условия устойчивости / А. С. Чепурненко, Б. М. Языев // Научное обозрение. - 2012. - № 6. - С. 202-204.
10. Маневич, А. И. Оптимальные центрально сжатые стержни открытого профиля / А. И. Маневич, С. В. Ракша // Theoretical Foundations of Civil Engineering - VІІІ: Ed. by W. Szczsniak, OW PW Warsaw. - 2000. - С. 484-489.
11. Леонтьевская, Е. Д. Оптимизация формы поперечного сечения стержней при ограничениях по устойчивости и прочности на сжатие / Е. Д. Леонтьевская, Б. А. Тухфатуллин, Л. Е. Путеева // Избранные доклады 62-й университетской научно-технической конференции студентов и молодых ученых. - 2016. - С. 41-44.
12. Ляхович, Л. С. Особые свойства форм потери устойчивости стержней минимальной материалоемкости при ограничении величины критической нагрузки для случаев линейной зависимости моментов инерции сечений и функции цели от варьируемого параметра / Л. С. Ляхович //Вестник Томского государственного архитектурно-строительного университета. - 2011. - №. 4. - С. 106-112.
13. Федоров, И. М. Оптимизация формы стержней при неконсервативном нагружении по критерию потери устойчивости / И. М. Федоров, Ю. М. Темис // Проблемы прочности и пластичности. - 2007. - №. 69. - С. 24-37.
14. Gill, P. E. SNOPT: An SQP algorithm for large-scale constrained optimization / P. E. Gill, W. Murray, M. A. Saunders //SIAM review. - 2005. - Т. 47. - №. 1. - С. 99-131.
15. Biggs, M.C. Constrained Minimization Using Recursive Quadratic Programming // Towards Global Optimization (L.C.W. Dixon and G.P. Szergo, eds.), North-Holland. - 1975. - Pp. 341-349.
16. Nocedal, J. Numerical Optimization, Second Edition / J. Nocedal, S. J. Wright. Springer Series in Operations Research, Springer Verlag, 2006. - 664 p.
17. Антоненко, Э. В. Эффективность сжатых стержней / Э. В. Антоненко, Н. С. Хлопцева //Математика. Механика. - 2007. - №. 9. - С. 124-126.
18. Егоров, Ю. В. О задаче Лагранжа об оптимальной форме колонны / Ю. В. Егоров // Доклады Академии наук. - Федеральное государственное бюджетное учреждение "Российская академия наук", 2003. - Т. 392. - №. 5. - С. 598-602.
19. Егоров, Ю. В. Об оптимальной форме колонны / Ю. В. Егоров, В. А. Кондратьев //Доклады Академии наук. - Российская академия наук, 1996. - Т. 350. - №. 6. - С. 727-729.
20. Гончаров, В. Ю. Некоторые осцилляционные свойства решений в задаче о потере устойчивости колонны / В. Ю. Гончаров, Л. А. Муравей //Дифференциальные уравнения, математическое моделирование и вычислительные алгоритмы. - 2021. - С. 90-92.


















