Россия
Москва, г. Москва и Московская область, Россия
Россия
УДК 519.8 Исследование операций
УДК 531 Общая механика. Механика твердых тел
УДК 534 Механические колебания. Акустика
УДК 539.2 Свойства и структура молекулярных систем
УДК 539.6 Межмолекулярные силы
УДК 620.9 Общая энергетика
УДК 624.042 Расчет нагрузок и напряжений
УДК 624.044 Расчет деформаций
УДК 699.8 Мероприятия по защите зданий, сооружений и конструкций. Изоляционные работы. Противоаварийные мероприятия
Амплитудно-частотные характеристики колебаний конструктивных элементов зданий и сооружений являются важными расчетными параметрами при анализе изменений напряженно-деформированного состояния здания в процессе эксплуатации, в том числе при проведении обследований и мониторинга технического состояния здания. Стандартизация метода определения значений этих параметров проводится в соответствии с требованиями ГОСТ 8.009 для обеспечения соблюдения требований ГОСТ 31937 и ГОСТ 32019. Колебания здания представляют собой суперпозицию собственных и вынужденных колебаний, вызванных различными внутренними (работой бытовой техники и различных технических систем здания) и внешними (городским транспортом, стройками и т. п.) воздействиями. Для определения значений периода, как правило, регистрируют собственные колебания здания, вызванные естественным динамическим природно-техногенным фоном города (при наличии оборудования, чувствительного к уровням естественного динамического воздействия), поэтому в процессе измерений дополнительных воздействий на здание не оказывают. Для зданий промышленного назначения характерны наличие и перемещение внутри зданий тяжелого технологического оборудования. Напряжения при колебаниях имеют знакопеременный характер, потому они могут вызывать усталость материала, из которого изготовлено сооружение. Это, в свою очередь, приводит к разрушению отдельных элементов сооружения и, как следствие, к авариям. В работе представлен динамический расчет элементов сооружения, состоящий из нескольких этапов: определены динамических характеристики узлов соединений конструктивов друг с другом; определены динамические степени свободы; формализован теоретический расчет на колебания.
динамика, устойчивость, собственные колебания, амплитуда, угловая частота, собственные числа, собственный вектор
Введение
Динамический расчет [1] в работе проведен для проверки формализованных алгоритмов динамических расчётов допустимости внутренних усилий и перемещений с точки зрения выполнения требований прочности, жесткости и выносливости, санитарно-гигиенических норм, технологии производства ]2,3]. При невыполнении допустимых норм возникает необходимость в уменьшении уровня колебаний. Из-за различных внешних воздействий на здания и сооружения и их конструктивные элементы, а также из-за динамических реакций конструктивных элементов и зданий в целом на эти воздействия, - элементы зданий подвержены сложным импульсным динамическим колебательным процессам с различными частотами и амплитудами. Предполагаемый вариант поведения конструктивов здания представлен на рис.1:
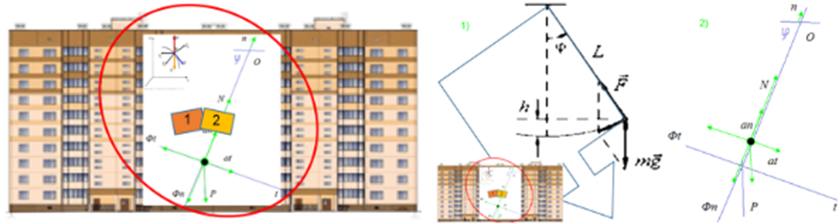
Рис.1. Вариант колебаний конструктивных элементов зданий с представлением колебательных процессов соответствующими расчётными схемами
Целью настоящей работы является возможная формализация и автоматизация процесса поиска динамических реакций элементов зданий и сооружений на внешние импульсные воздействия разной природы.
Методы исследований
Для определения динамических взаимодействий изучаемых объектов друг с другом и с несущим остовом здания [4,5] разработана специальная схема, рис. 2:
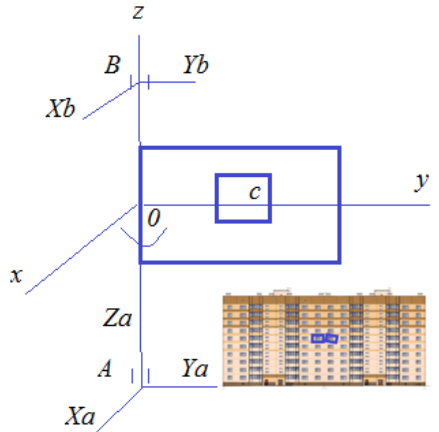
Рис. 2. Расчётная схема для определения динамических реакций связей
при возможном вращении элементов здания вокруг вертикальной оси «Z»,
Уравновешивание приведенной на рис. 2 системы сил выполняется в точках «А» и «В». Поэтому, эти точки представляются концентраторами реактивных сил на внешние воздействия. Составив проекционные условия кинетостатического равновесия [6], получим систему уравнений равновесия сил и моментов:
$X_{Адин}+X_{Вдин}+my_C \ddot φ +mx_C \dot φ^2=0$
$Y_{ Адин}+Y_{ Вдин} + my_ C \ddot φ + my_ C \dot φ^ 2 =0$
$Z_{ Адин}=0$
$Y_{ Адин}|Z_A|+ Y_{ Вдин}|Z_B| + I_{xz} C \ddot φ - I_{yz}C \dot φ^ 2 =0$
$-X_{ Адин}|Z_A|+ X_{ Вдин}|Z_B| + I_{yz} C \ddot φ - I_{xz}C \dot φ^ 2 =0$
где XАдин, XВдин, YАдин, YВдин — соответствующие динамические реакции связей в форме реакции на импульсные динамические воздействия. Формализованная реализация алгоритма символьного решения системы уравнений равновесия представлена на рис. 3:

Рис. 3. Реализация формализации алгоритма
символьного нахождения динамических реакций связей в точках «А» и «В»
Очевидно, что характер взаимодействия связей на расчетной схеме, а по существу узлов крепления с несущими конструкциями зданий, носит явно выраженный импульсно-динамический характер {7}. Построим эпюры динамических воздействий (М) [8,9] при двух частотах возмущающей нагрузки:
Таблица 1
|
1, м |
h, м |
q, кН/м |
Р, кН |
m, кНм |
|
9 |
6 |
1 |
20 |
30 |
Составим расчётную схему, рис. 4:
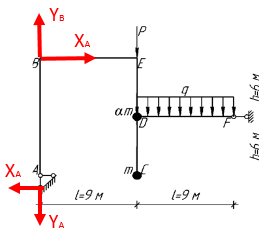
Рис. 4. Расчётная схема узла соединения элементов здания
с сосредоточенными в точках «А» и «В» массами
Результаты исследований
Число степеней свободы массы приведенной системы: n = 2. Величина сосредоточенных масс: m1 = m; m2 = m + a m = m + 2m = 3m. Составим частотное уравнение. Определим спектр частот собственных колебаний. Найдём формы собственных колебаний. Запишем уравнения частот в общем виде:
$\begin{pmatrix}
δ_{11}∙m_1-μ_1 & δ_{12}∙m_1 \\
δ_{21}∙m_2 & δ_{21}∙m_2-μ_2 \\
\end{pmatrix}=0$;
$μ=\frac{1}{ω^2}$
Приложим единичные усилия по направлению колебаний сосредоточенных масс, построим единичные эпюры моментов, и определим коэффициенты указанного «векового» уравнения, рис. 5:
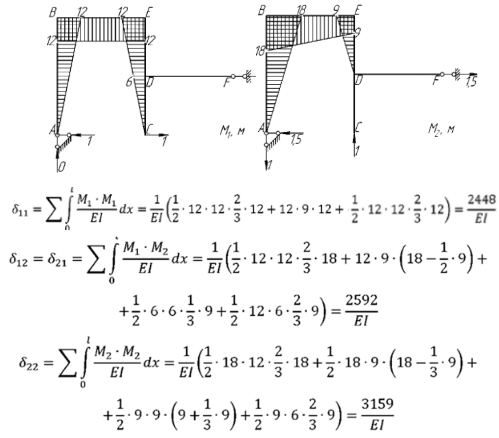
Рис. 5. Определение коэффициентов уравнения
Составим характеристическое уравнение:
$(μ_1)^2-\frac{11925∙m}{EI}∙μ_1+\frac{3044304∙m^2}{EI^2}=0; μ_1=\frac{11664∙m}{EI}; μ_2=\frac{261∙m}{EI}$
Определим частоты собственных колебаний конструктивов узла:
$ω_1=\sqrt{\frac{1}{μ_1}}=\frac{1}{108}∙\sqrt{\frac{EI}{m}} ; ω_2=\sqrt{\frac{1}{μ_1}} =frac{1}{16.155}∙\sqrt{\frac{EI}{m}}$;
Выберем минимальное значение из двух значений частот собственных колебаний:
$ω_{min}=ω_1=\sqrt{\frac{1}{μ_1}=\frac{1}{108}∙\sqrt{\frac{EI}{m}$;
Формы колебаний найдём, переписав систему уравнений следующим образом:
$\begin{pmatrix}
(δ_{11}∙m_1-μ_1)∙v_1 & (δ_{12}∙m_1)∙v_{2i} \\
δ_{21}∙m_2∙v_1 & (δ_{21}∙m_2-μ_2)∙v_{2i} \\
\end{pmatrix}=0$;
Будем считать, что
Будем считать, что (i=2)
Представим обе формы колебаний рис. 6:
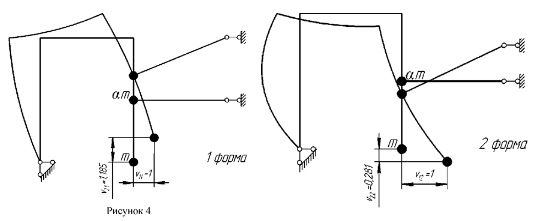
Рис. 6. Первая и вторая формы найденных колебаний
Построим эпюру моментов от амплитудных нагрузок, рис. 7:
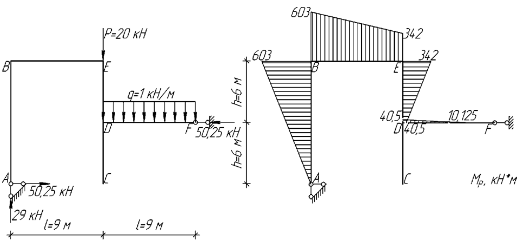
Рис. 7. Эпюры моментов от амплитудных нагрузок
Определяем свободные члены системы канонических уравнений, рис. 8:
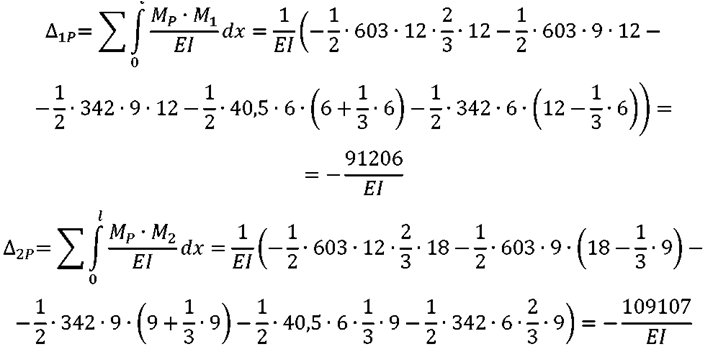
Рис. 8. Формализованный алгоритм и значения свободных членов системы канонических уравнений
Запишем систему канонических уравнений для определения амплитудных значений инерционных сил:
$\begin{cases}
δ_{11}^*∙x_1+δ_{12}∙x_2+∆_{1p}=0 \\
δ_{22}∙x_1+δ_{22}^*∙x_2+∆_{2p}=0
\end{cases}$
Вычислим главные коэффициенты системы канонических уравнений:
Тогда
$δ_{11}^*=δ_{11}=-\frac{1}{m_1∙θ^2}=\frac{2448}{EI}-\frac{1}{m∙\frac{1}{135}∙\sqrt\frac{EI}{m}0^2}=-\frac{2916}{EI}$
$δ_{22}^*=δ_{22}=-\frac{1}{m_2∙θ^2}=\frac{3159}{EI}-\frac{1}{3m∙\frac{1}{135}∙\sqrt\frac{EI}{m}0^2}=-\frac{2916}{EI}$
Решая систему канонических уравнений определяем амплитудные значения инерционных сил x1 = -13,968 [кН] и x2 = -49,833 [кН]. Теперь можно построить «исправленную» динамическую эпюру моментов, рис.10, с учётом
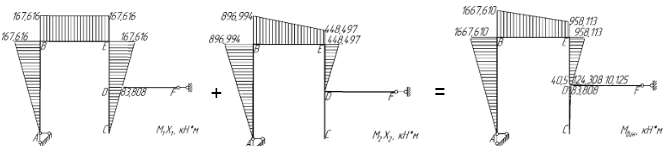
Рис. 9. Построение динамической эпюры моментов
Заключение
Вывод 1. Задача расчёта на импульсную динамическую нагрузку узла соединения элементов здания формализована.
Вывод 2. Задача расчёта на импульсную динамическую нагрузку узла соединения элементов здания автоматизирована.
1. Калинин, А.А., Петухов, В.В. Колебания упругой системы с двумя степенями свободы : курс лекций / А.А. Калинин, В.В. Петухов - Витебск: УО"ВГТУ", 2009. - 69с.
2. Масленников А.М. Основы динамики и устойчивости стержневых систем: Учеб. пособие /ООО “Изд-во АСВ”, СПб гос.архит.-строит.ун-т,-М.; СПб., 2000.-204 с.
3. Бутенин Н.В. и др. Курс теоретической механики: Учеб.пособие для студ-ов вузов по техн. спец.:В 2-х т./ Н.В.Бутенин, Я.Л.Лунц, Д.Р.Меркин. СПб.:Лань.-5-е изд., испр. 2008.-729 с EDN: https://elibrary.ru/QJTVUT
4. Численные методы решения задач строительной механики: Справ. пособие / В. П. Ильин, В. В. Карпов, А. М. Масленников; Под общ. ред. В. П. Ильина. - Минск: Вышэйш. шк., 1990. - 349 с. EDN: https://elibrary.ru/UGDTKB
5. Тарг С.М. Краткий курс теоретической механики: Учеб. для втузов/С.М.Тарг.-15-е изд., стер. - М.: Высш. шк., 2008.-415 с. EDN: https://elibrary.ru/QJSWJP
6. Феодосьев В.И. Сопротивление материалов: Учебник для студ-ов высш.техн.учеб.зав. - 10-е изд., перераб. и доп. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. - 588 с.
7. Смирнов А.Ф. Устойчивость и колебания сооружений. - М.: Трансжелдориздат, 1958. -572с
8. Канторович Л.В., Крылов В.И. Приближенные методы анализа. - М.: Гостехиздат, 1952. 692 с.
9. Лукашевич А.А. Современные численные методы строительной механики: Учебное пособие. - Хабаровск: Изд-во Хабар. гос. техн. ун-та, 2003. - 135 с. EDN: https://elibrary.ru/QNKIVB


















