Moskva, Moscow, Russian Federation
Russian Federation
UDK 691 Строительные материалы и изделия
The paper proposes a method for determining the estimated parameter of the stability state of discrete systems exposed to external influences. As a rule, the loss of stability of the first and second kind leads to a problematic operation process throughout the life cycle, or even the destruction of the system. Hence the requirements of a certain rigidity to the designed and operated systems in order to ensure their geometric immutability. At the same time, in practice, there are no naturally deformable systems from external influences. The paper sets and solves the problem of determining the stability parameter, with the help of which, even before the stage of loss of stability, it is possible to predict the future state of a discrete system, i.e. to predict whether it (the system) has sufficient internal properties to return to a stable position at any exit from the preliminary state of equilibrium due to the influence of external forces.
discrete systems, conservative forces, stability, loss of stability, critical stability parameter, reduced length, reference effects, bifurcation point, supercritical deformation
Введение
В некоторых случаях, например при эксплуатационном увеличении нагрузки сверх определённой величины, или при любом другом случайном импульсном или динамическом воздействии на объекты, его конструктивные элементы могут внезапно потерять свою так называемую устойчивость положения или формы.
Переход устойчивого состояния в состояние неустойчивого равновесия будем называть потерей устойчивости. Границу перехода в состояние неустойчивого равновесия обозначим - критическим состоянием. Внешние воздействия, приводящие объекты к критическим состояниям, - будем считать критическими силами.
При этом будем считать, что равновесия положения или формы на протяжении всего жизненного цикла - устойчивыми, если при любых воздействиях, элементы рассматриваемых объектов всё-таки деформируясь от этих воздействий, но тем не менее, - сохраняют свойства и тенденции к восстановлению как своих геометрических размеров, так и эксплуатационных качеств.
Допущения, принятые в работе.
1. Силы консервативны;
2. Рассматриваемые виртуальные конструкции работают упруго;
3. Модули всех величин внешних воздействий приняты равными условной единице.
Определение.
Уточним цели и задачи работы на основе следующих понятий. Как интерпретировать понятие «устойчивость»? Определим это понятие, как способность систем восстанавливать своё равновесное состояние. Тогда потеря устойчивости, - это потеря способности восстанавливать своё равновесное состояние.
Таким образом система: а) после воздействия может вернуться в исходное равновесное состояние; b) после воздействия может вернуться в новое равновесное состояние; с) после воздействия может не вернуться в исходное равновесное состояние;
Цели и задачи.
- Оценить состояния системы до наступления состояния потери устойчивости;
- Предложить критерии для предварительной оценки потери устойчивости;
- Представить прогноз поведения анализируемой системы.
Пусть задана система, находящаяся в равновесии рис. 1.
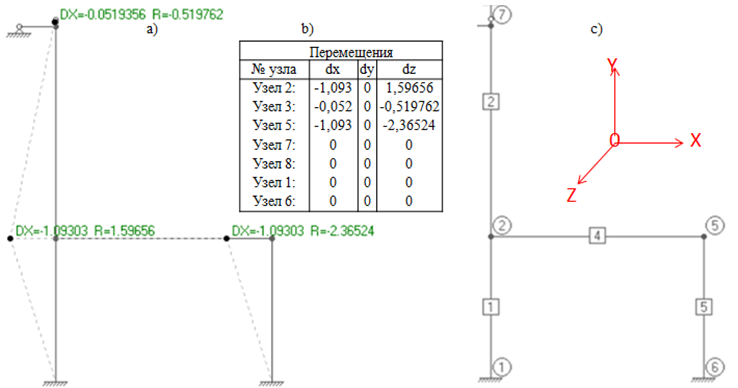
Рис.1. Геометрия заданной схемы (а), принятая кодировка узлов и стержней (b), расчётная схема (с) анализируемой системы.
Для разработки критериев оценки состояния на основе точного графоаналитического расчёта определим внутренние усилия N, Q и M, как напряженно деформированное состояние системы (НДС), возникающие в анализируемой системе, рис.1a,b от внешних воздействий.
Результаты расчётов НДС анализируемой системы и перемещений узлов элементов, приведены в таблицах 1, 2, 3, 4,
Таблица1
Моменты
|
Элемент 1: |
M(2) = 2.00644 |
M(1) = 1.20816 |
|
Элемент 2: |
M(2) = 0.717602 |
M(3) = 0.0121627 |
|
Элемент 4: |
M(2) = -2.72404 |
M(5) = 1.95536 |
|
Элемент 5: |
M(5) = -1.95536 |
M(6) = -0.772736 |
|
Элемент 6: |
M(3) = -0.0121627 |
M(7) = 0 |
|
Элемент 7: |
M(7) = 0 |
M(8) = 0 |
Таблица 2
Поперечные силы
|
Элемент 1: |
Q(2) = -0.803651 |
Q(1) = -0.803651 |
|
Элемент 2: |
Q(2) = -0.121627 |
Q(3) = -0.121627 |
|
Элемент 4: |
Q(2) = 3.12811 |
Q(5) = -2.87189 |
|
Элемент 5: |
Q(5) = 0.682023 |
Q(6) = 0.682023 |
|
Элемент 6: |
Q(3) = 0.121627 |
Q(7) = 0.121627 |
|
Элемент 7: |
Q(7) = 0 |
Q(8) = 0 |
Таблица 3
Продольные силы
|
Элемент 1: |
N(2) = -5.12811 |
N(1) = -5.12811 |
|
Элемент 2: |
N(2) = -1 |
N(3) = -1 |
|
Элемент 4: |
N(2) = -0.682023 |
N(5) = -0.682023 |
|
Элемент 5: |
N(5) = -3.87189 |
N(6) = -3.87189 |
|
Элемент 6: |
N(3) = 0 |
N(7) = 0 |
|
Элемент 7: |
N(7) = 0.121627 |
N(8) = 0.121627 |
Таблица 4
Перемещения
|
Узел 2: |
dx = -1.09303 |
dy = 0 |
da = 1.59656 |
|
Узел 3: |
dx = -0.0519356 |
dy = 0 |
da = -0.519762 |
|
Узел 5: |
dx = -1.09303 |
dy = 0 |
da = -2.36524 |
|
Узел 7: |
dx = 0 |
dy = 0 |
da = 0 |
|
Узел 8: |
dx = 0 |
dy = 0 |
da = 0 |
|
Узел 1: |
dx = 0 |
dy = 0 |
da = 0 |
|
Узел 6: |
dx = 0 |
dy = 0 |
da = 0 |
На основе полученных расчётных данных построим графики изгибающих моментов М. Далее, используя дифференциальные зависимости между параметрами (НДС) вида 
построим графики перерезывающих сил Q, рис. 2:
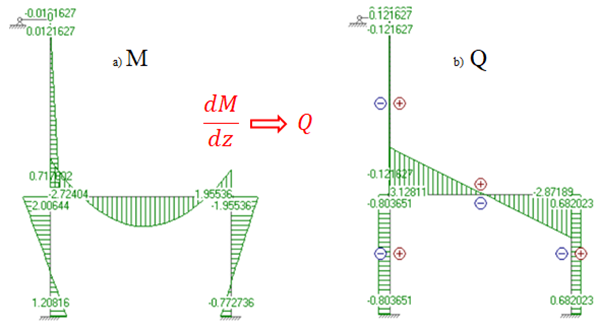
Рис. 2 Графики изгибающих моментов М (а) и графики перерезывающих сил Q (b) анализируемой системы
Путем анализа узловых значений ординат графика Q, построенного на предыдущем этапе, производится расчёт и построение узловых ординат продольных сил N, рис. 3:
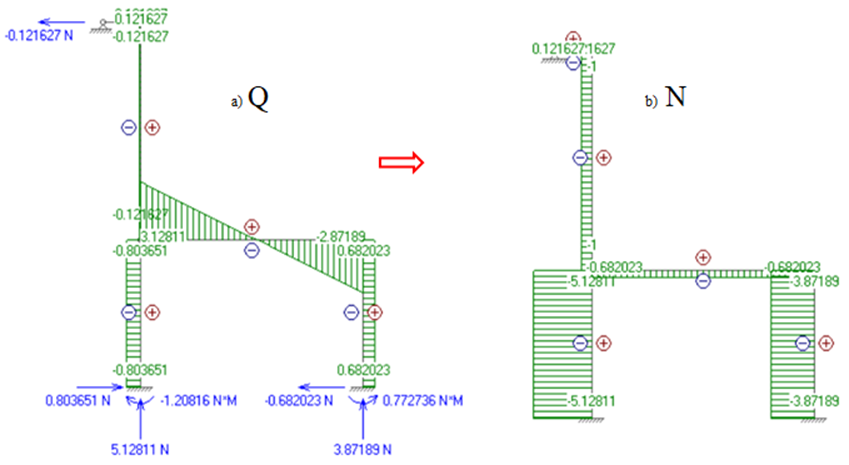
Рис. 3 Построение графиков продольных сил N (b) на основе графиков перерезывающих cил Q(a) для анализируемой системы
С учётом предыдущих действий построим деформационную схему поведения анализируемой системы от приложенных воздействий, рис. 4:
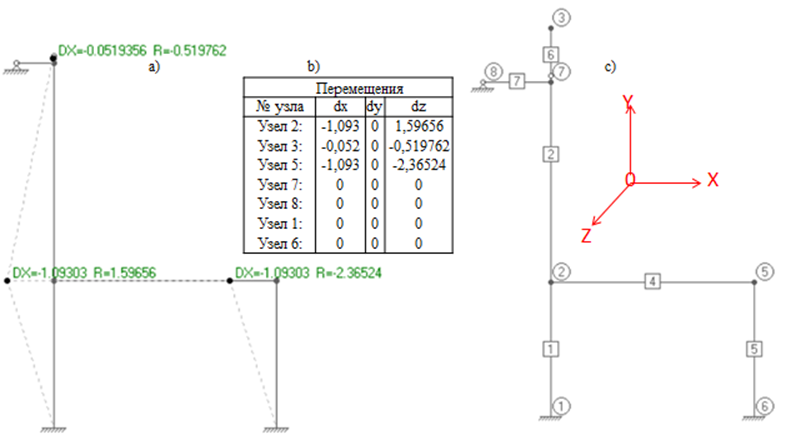
Рис. 4. (а) Виртуальные деформации узловых точек элементов анализируемой системы (Схема потери устойчивости формы). (b) Таблица деформаций. (с) Схема кодировки элементов в локальной системе координат.
Для обоснования критерия предварительной оценки состояния системы, используя принцип суперпозиции, рассмотрим поведение каждого из четырех элементов, №1, №2, №4 и №5, (на рис. 4) каждого по отдельности.
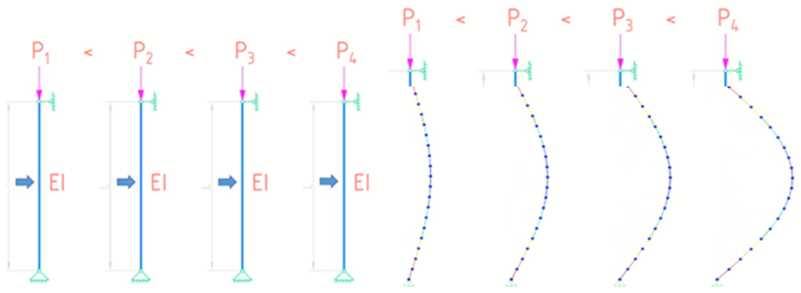
Рис. 5 Виртуальный тест на устойчивость
Рассмотрим условный тест на устойчивость для элементов одинаковой жесткости, расположенных слева направо по мере увеличения сжимающего воздействия P. Изначально все элементы находятся в равновесии. В качестве возмущающего воздействия, - показано боковое одноразовое импульсное воздействие, которое приводит к деформации рассматриваемых элементов. Наблюдаем, что не все элементы одинаково возвращаются в исходное состояние (см. рис. 5)
Задача состоит в том, чтобы заранее, еще до потери устойчивости установить такой оценочный параметр, - который заранее сможет указать те из элементов, которые после деформации (т.е. после снятия внешнего воздействия) будут способны вернуться в начальное равновесное состояние, не потеряв устойчивость.
Дискретные системы. Решение задачи с угловой пружиной жесткостью k.
Представим каждый элемент из анализируемой системы вертикальным элементом, колонной, - длиной L. В качестве примера расчёта, выберем элемент №4 анализируемой системы (Рис.4). Приложим к нему сжимающее воздействие P. Введем понятие базовой, референт силы (Pref). Ему (Pref) поставим в соответствие эталонную продольную силу (N) величиной, равной условной единице (
Закрепим шарниром колонну в точке B, придав ей вертикальное положение. Предположим, что колонна удерживается в вертикальном положении свойствами собственной бесконечной жесткости, а в случае отклонения от вертикальной оси, возвращается в исходное вертикальное положение при помощи виртуальной угловой пружины жесткостью k.
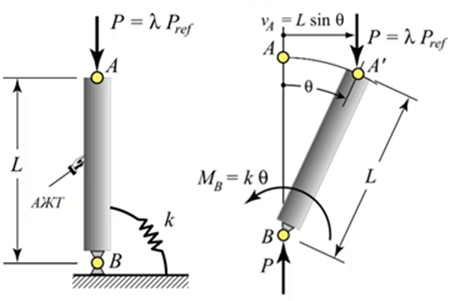
Рис. 6 Расчетная схема потери устойчивости анализируемых элементов №1,2,4,5 (рис. 4) условно абсолютной жесткости с угловой пружиной, жесткостью k
Отклонение от вертикального положения возможно на любой угол 
. При отклонении на угол
При отклонении колонны от вертикального положения, на неё будут действовать дестабилизирующие (возмущающее) воздействия в виде крутящего момента относительно точки B направленного по часовой стрелке. Момент будет пытаться вывести систему из предварительного состояния равновесия. Кроме этого на рассматриваемую систему будет воздействовать восстанавливающий крутящий момент относительно указанной точки B, направленный против часовой стрелки, связанный с пружиной в точке B жесткостью k. Возврат в исходное равновесие (виртуально) обеспечивается жесткостью угловой пружины. Если удалить пружину (виртуально), тогда возврат в исходное равновесное состояние должен будет обеспечиваться жесткостью k самой колонны.
Выход из состояния равновесия возможен из-за воздействия дестабилизирующего момента, а возврат в исходное состояние возможен из-за восстанавливающего момента. Рассмотрим условие их равенства друг другу, т.е. условие сохранения равновесия анализируемой системы (см. рис.6).
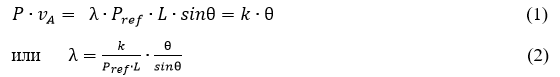
Установим соотношения между 
и
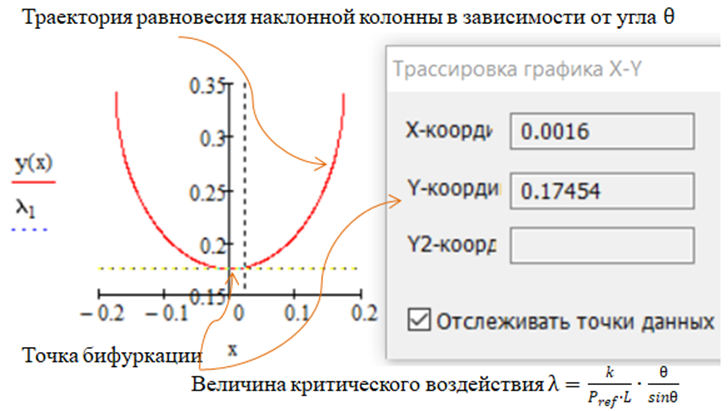
Рис. 7 Диаграмма изменения состояния равновесия с угловой пружиной с помощью оценочного параметра 
в зависимости от угла наклона 
Таким образом, колонна, как абсолютно жесткий элемент, потенциально может находиться в состояниях равновесия будучи в вертикальном положении и, будучи в наклонном положении на определённый угол .
На рис.7 указана точка бифуркации, которая в данном случае может представлять собой индикатор возможной потери устойчивости еще до момента практической потери устойчивости элементом при виртуальных изменениях соотношений между и .
Дискретные системы. Решение задачи с линейной пружиной жесткостью k.
Так же, как и в предыдущем случае, введем понятие референт силы (Pref). Так же этому понятию (Pref) поставим в соответствие эталонную продольную силу (N) величиной, равной условной единице (
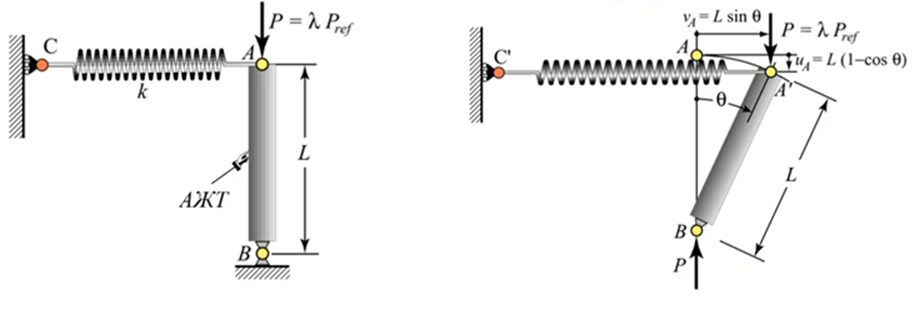
Рис. 8 Расчетная схема потери устойчивости анализируемых элементов №1,2,4,5 (рис. 4) условно абсолютной жесткости с линейной пружиной жесткостью k
Предположим, что рассматриваемые элементы занимают вертикальное положение, как это показано на рис. 5, 6. Предположим, что элементы закреплены к опорам, как это показано на рис. 8.
Представим, что все элементы рассматриваемой системы абсолютно жесткие. Тогда, элементы не будут деформироваться так, как это показано на рис. 5, а будут отклоняться от своей геометрической оси на любой угол θ, как это показано на рис.8. Причём, отклонение на угол
Согласно приведенной расчётной схеме, даже при незначительном отклонении элемента от вертикального положения, на него будут воздействовать дестабилизирующие воздействия в виде крутящего момента относительно точки B направленный по часовой стрелке. Этот момент будет пытаться вывести систему из состояния равновесия. Помимо дестабилизирующего момента, на систему будет воздействовать восстанавливающий крутящий момент относительно точки B, направленный против часовой стрелки, связанный с опорой в точке A в виде линейной пружины CA жесткости k. Возврат в исходное равновесие (виртуально) обеспечивается жесткостью линейной пружины. Если удалить (виртуально) указанную пружину, тогда возврат в исходное равновесное состояние должен обеспечиваться жесткостью самого рассматриваемого элемента AB.
С учётом этого рассмотрим условие равенства друг другу дестабилизирующего и восстанавливающего моментов.
Условие равновесия представим, как равенство нулю суммы моментов всех сил относительно точки B (рис. 8):
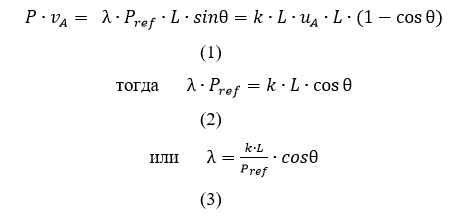
Покажем соотношения между и , рис. 9:
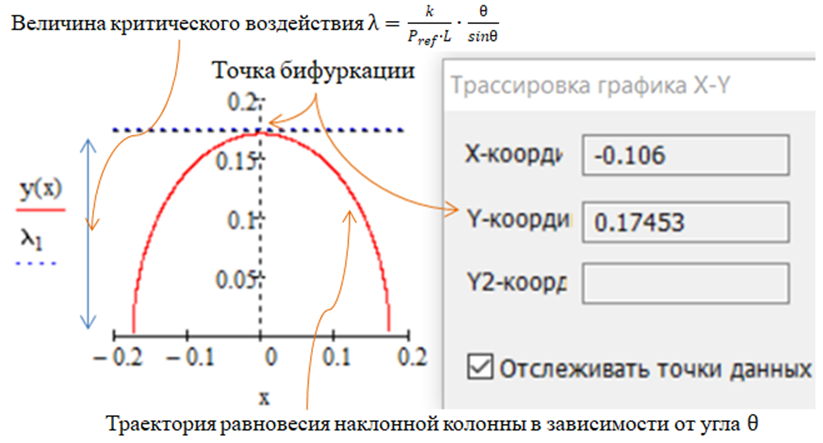
Рис. 9 Диаграмма изменения состояния равновесия с угловой пружиной с помощью оценочного параметра в зависимости от угла наклона
Элемент AB, как абсолютно жесткая колонна согласно рис. 9 может находиться и в состояниях равновесия и будучи и в вертикальном положении и, будучи в наклонном, на определённый угол , положении. На диаграмме отмечена точка бифуркации, которая в данном случае может представлять собой индикатор возможной потери устойчивости еще до момента практической потери устойчивости элементом при виртуальных изменениях соотношений между и .
Гипотеза. Сравнивая диаграммы на рис. 7, 9 друг с другом, полученные на основе расчёта анализируемой системы (рис.4), приходим к выводу о том, что расположение точек бифуркации анализируемых систем, как в первом, так и во втором случаях в зависимости от соотношений между и выше значений критических сил (параметров) может быть использовано при осуществлении прогноза поведения анализируемых систем. Рис. 7, 9 указывают на то, что закритическая деформация и в первом и во втором случае после точки бифуркации возможна, и значит анализируемая система (рис.1) обладает потенциальной энергией возврата в равновесное состояние после выхода из состояния равновесия.
Результаты расчетов и определения критических сил приведены в таблице 8:
Таблица 5
Примечание: Во всех указанных элементах критические силы меньше вычисленных ранее НДС (P<Pc), что указывает на то, что анализируемая на рис. 1 система находится в состоянии устойчивого равновесия
Выводы:
- Произведена аналитическая оценка состояния системы на потерю устойчивости формы.
- Предложен критерий предварительной оценки потери устойчивости системы в виде диаграммы состояния дискретной системы (рис. 7,9).
- Анализируемая система (рис.1) находится в устойчивом равновесии (табл. 9)
1. Bityurin A.A., Manzhosov V.K. Modelirovanie prodol'nogo udara odnorodnyh sterzhney pri neuderzhivayuschih svyazyah //Vestnik UlGTU.- 2005.- № 3. - S. 23-25.
2. Vol'mir A.S. Ustoychivost' uprugih sistem. -M.: GITTL, 1962.-880 s.
3. Darkov A.V., Shpiro G.S. Soprotivlenie materialov.- M.: Vysshaya shkola, 2003.- 641 s.
4. Lavrent'ev M.A., Ishlinskiy A.Yu. Dinamicheskie formy poteri ustoychivosti uprugih sistem //Doklady AN SSSR.-1949. -T. 65, № 6. -S. 42-45.
5. Malyshev B.M. Ustoychivost' sterzhnya pri udarnom szhatii // Izvestiya AN SSSR. MTT. -1966. -№ 4. - S. 137-142.
6. Bityurin A.A., Manzhosov V.K. Prodol'nyy udar neodnorodnogo sterzhnya o zhestkuyu pregradu // Ul'yanovsk: Izd-vo UlGTU, 2009.- 164 s.
